Найти центр тяжести ус

§ 8.3. Центр тяжести

Центр тяжести

Момент силы зависит от ее плеча, а значит, и от точки приложения силы. Когда на тело действуют силы со стороны тросов, пружин и т. п., то положение точек приложения сил очевидно. Но что можно сказать о точке приложения силы тяжести?

Особенностью силы тяжести является то, что она действует на тело не в одной какой-то точке, а по всему объему тела. Силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и, следовательно, строго говоря, не будут параллельными. Однако размеры всех сооружений на Земле значительно меньше ее радиуса. Поэтому практически все эти силы можно считать параллельными.

Точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве), называется центром тяжести.

Определение центра тяжести тела простой формы

Найдем вначале положение центра тяжести для наиболее простого случая, когда тело состоит из двух шаров различных масс, соединенных стержнем, массой которого можно пренебречь по сравнению с массами шаров. Кроме того, длину стержня будем считать значительно превышающей радиусы шаров. Тогда шары можно считать материальными точками (рис. 8.4, а).

Итак, на материальные точки А и Б, соединенные невесомым стержнем, действуют силы тяжести ₁ и ₂, параллельные друг другу. Геометрическая сумма этих сил представляет собой результирующую силу тяжести:

Она направлена к центру Земли, так же как и силы ₁ и ₂, а ее модуль равен сумме модулей слагаемых сил.

Положение центра тяжести, т. е. точки приложения результирующей силы, можно определить, используя тот простой факт, что тело, закрепленное на оси, проходящей через центр тяжести С, должно находиться в равновесии. Ведь относительно этой оси моменты сил тяжести _т и силы реакции опоры равны нулю, так как равны нулю плечи этих сил (рис. 8.4, б).

С другой стороны, согласно условию равновесия (8.2.5), можно записать: F₁d₁ — F₂d₂ = 0, где d₁ = АС и d₂ = СВ — плечи сил ₁ и ₂. Отсюда

Равенство (8.3.2) определяет положение центра тяжести рассматриваемого тела. Точка приложения равнодействующей параллельных сил тяжести делит расстояние между точками приложения этих сил на отрезки, обратно пропорциональные модулям сил.

Нахождение центров тяжести тел является важной технической задачей, так как от положения центров тяжести зависит устойчивость мостов, плотин, зданий, телевизионных вышек, автомашин, ракет на старте и т. п. Нужно поэтому познакомиться с методами нахождения центров тяжести тел различной формы.

Нахождение центра тяжести тел

В технике и повседневной жизни мы встречаемся с телами самой различной формы. Часто они состоят из стержней и дисков (колесо на оси, спортивная штанга и т. д.). Многие плоские фигуры состоят из прямоугольных и треугольных пластин. При определении положения центра тяжести подобных тел проще всего вначале определить положение центров тяжести отдельных его частей простой формы. У тел простой формы можно сразу указать положение центра тяжести, руководствуясь соображениями симметрии.

Так, центр тяжести однородного стержня, очевидно, располагается в середине стержня (рис. 8.5). У всех однородных фигур, имеющих центр симметрии, центр тяжести совпадает с этим центром: у круга — с его геометрическим центром, у параллелограмма — с точкой пересечения диагоналей и т. д. При этом центр тяжести может находиться и вне тела (например, у кольца или пустотелой сферы).

Определив положения центров тяжести составных частей тела сложной формы, можно найти, где расположен центр тяжести всего тела. Для этого надо заменить тело системой материальных точек, каждая из которых помещается в центре тяжеети соответствующей части тела и имеет массу этой части (рис. 8.6).

Координаты центра тяжести твердого тела

Рассмотрим теперь общий метод определения координат центра тяжести произвольного твердого тела. Для решения задачи предположим, что равнодействующая сил тяжести, приложенных к отдельным элементам тела, и точка ее приложения уже найдены.

Пусть сила тяжести равна _т и приложена в точке С (рис. 8.7) с координатами х, y, z. Приложим теперь к телу в другой точке внешнюю силу такую, чтобы тело находилось в равновесии. Это можно сделать, например, подвесив тело в точке D на нити или закрепив в этой точке другим способом. Так как в этом случае можно считать, что на тело действуют только две силы и _т, то согласно условию равновесия (8.2.1):

Отсюда следует, что сила должна быть равна по модулю и противоположна по направлению силе _т.

Разобьем теперь мысленно тело на элементы (материальные точки) и запишем условие равновесия, уже не заменяя равнодействующей совокупность элементарных сил тяжести:

(здесь Δ_т1 = Δm₁ — сила тяжести, действующая на произвольный малый элемент массой Δm₁).

Из (8.3.3) и (8.3.4) следует, что

(здесь m = — масса тела).

Таким образом, равнодействующая направлена вниз и равна сумме всех элементарных сил тяжести.

Вспомним теперь, что рассматриваемое тело находится в покое. Это значит, что совокупное действие силы и силы _т, заменяющей многочисленные элементарные силы тяжести, не вызывает вращения тела. Следовательно, выполняется условие равновесия (8.2.4) для моментов всех сил относительно любой неподвижной оси. В качестве таковой удобно взять одну из координатных осей, например ось OZ (рис. 8.8). Момент М равнодействующей _т и момент М’ силы должны в сумме давать при равновесии нуль:

Очевидно, что условие (8.3.5) сводится к требованию, чтобы равные по модулю и противоположные по направлению силы и _т имели бы одну и ту же линию действия.

В то же время если не заменять элементарные силы тяжести равнодействующей, то условие равновесия (8.3.5) для моментов должно выполняться в виде

Из уравнений (8.3.5) и (8.3.6) следует, что

т. е. момент равнодействующей относительно какой-нибудь неподвижной оси равен сумме моментов всех элементарных сил тяжести относительно той же оси.

Подсчитаем упомянутые моменты сил относительно оси OZ. Как известно, момент силы равен произведению силы на плечо. Для силы Δ_тi плечом является координата x_i элемента малой массы Δmi (см. рис. 8.8). Поэтому момент силы Δ_тi равен: Δ_тix_i = Δm_ix_ig, а общий момент всех сил тяжести равен:

Мы предположили, что точка, в которой приложена суммарная сила _т, имеет координату х. Тогда суммарная сила создает момент относительно той же оси OZ, равный

Поскольку этот момент должен быть равен моменту, определяемому по формуле (8.3.7), то

Отсюда для координаты точки приложения равнодействующей всех параллельных сил тяжести получаем:

Мы нашли только одну из координат точки приложения равнодействующей. Другие координаты остались неопределенными, что и понятно, поскольку найденную точку можно переносить, например, вверх или вниз без изменения момента сил относительно оси OZ.

Однако этот способ можно применить еще раз, повернув оси координат вместе с телом так, чтобы вверх теперь была направлена уже другая ось (рис. 8.9).

Найдем вторую координату точки приложения суммарной силы:

а затем и третью:

Координаты центра тяжести, следовательно, определяются по формулам (8.3.8), (8.3.9), (8.3.10). Если использовать векторную форму записи, то все эти три формулы будут эквивалентны одной:

Центр тяжести и центр масс

Нетрудно заметить, что формула (8.3.11) совпадает с выражениями (7.3.4), которые определяют положение центра масс тела. Таким образом, в случае, когда размеры тела малы по сравнению с расстоянием до центра земного шара, центр тяжести совпадает с центром масс тела.

Кроме того, очевидно, что высказанные положения применимы и к расчету положения точки приложения силы инерции при поступательном движении. В самом деле, для такого расчета мы можем аналогичным образом разбить тело на малые элементы, к каждому из которых будет приложена сила инерции — Δm_i, где — ускорение системы отсчета. Как и при нахождении центра тяжести, все силы инерции параллельны и пропорциональны массам отдельных элементов. Поэтому сила инерции в неинер-циальной системе отсчета, движущейся поступательно, приложена всегда к центру масс (центру тяжести) тела. Наоборот, центробежная сила инерции в общем случае не приложена к центру масс, так как из-за различных расстояний до оси вращения на элементы даже одинаковой массы действуют в неинерци-альной системе отсчета различные центробежные силы инерции.

Мы получили более полное представление о центре тяжести. Практически во всех встречающихся задачах центр тяжести тела совпадает с его центром масс.

Источник статьи: http://tepka.ru/fizika_10/107.html

Центр тяжести тела

Как известно, сила тяжести тела равна векторной сумме сил тяжести, которые действуют на все материальные точки, на которые можно разбить рассматриваемое тело. Точку, к которой приложена результирующая сила тяжести, называют центром тяжести. Если известно положение центра тяжести, то можно считать, что на тело действует только одна сила тяжести, приложенная к центру тяжести.

Следует учитывать, что силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и не являются строго параллельными. Но так как размеры большинства тел на Земле много меньше ее радиуса, поэтому эти силы считают параллельными.

Определение центра тяжести тела

Центром тяжести называют точку, через которую проходит равнодействующая всех сил тяжести, действующих на материальные точки, на которые разбито рассматриваемое тело, при любом положении тела в пространстве.

Центр тяжести — это точка, относительно которой суммарный момент сил тяжести равен нулю при любом положении тела.

От положения центра тяжести зависит устойчивость всех конструкций.

Как найти центр тяжести?

Для нахождения центра тяжести тела сложной формы необходимо мысленно разбить тело на части простой формы и определить место нахождения центров тяжести для них. У тел простой формы центр тяжести определяют, используя их симметрию. Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.

Определив, где расположены центры тяжести отдельных частей тела, переходят к поиску места расположения центра тяжести тела в целом. Тело представляют в виде системы материальных точек. При этом каждая точка имеет массу своей части тела и располагается в ее центре тяжести.

Координаты центра тяжести тела

В трехмерном пространстве координаты центра тяжести для твердого тела нахояд как:

где $m$ — масса тела.$;;x_i$ — координата на оси X элементарной массы $\Delta m_i$; $y_i$ — координата на оси Y элементарной массы $\Delta m_i$; ; $z_i$ — координата на оси Z элементарной массы $\Delta m_i$.

В векторной форме записи система уравнений (1) представляется как:

$<\overline>_c$ — радиус — вектор, определяющий положение центра тяжести; $<\overline>_i$ — радиус-векторы, которые определяют положения элементарных масс.

Центр тяжести, центр масс и центр инерции тела

Считают, что центр тяжести тела совпадают с центром масс тела, если его размеры малы в сравнении с расстоянием до центра Земли. При этом формулы, которые определяют положение цента тяжести и центра масс тела совпадают с выражениями (1) и (2). В основной массе задач центр тяжести принимают совпадающим с центром масс тела.

Сила инерции в неинерциальных системах отсчета, движущихся поступательно, приложена к центру тяжести тела.

Но центробежная сила инерции (в общем случае) не приложена к центру тяжести, поскольку в неинерциальной системе отсчета на элементы тела действуют разные центробежные силы инерции (даже если массы элементов равны), так как расстояния до оси вращения разные.

Примеры задач с решением

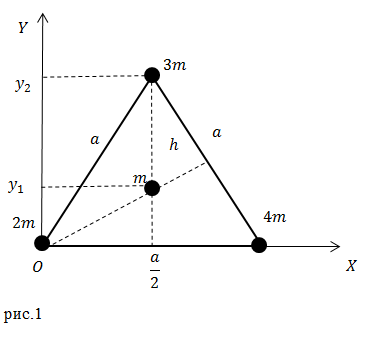
Задание: Каковы координаты центра тяжести системы из трех точечных масс, расположенных в вершинах и одной в центре равностороннего треугольника, со стороной равной $a\ (м)$ (рис.1)?

Решение: Определение для координат $x_c\ и\ y_c$ центра тяжести в нашем случае запишем в виде:

Из рис.1 мы видим, что соответствующие абсциссы точек равны:

Тогда абсцисса центра тяжести получается равной:

Найдем ординаты точек.

Для того чтобы найти ординату $y_2$ найдем, высоту в равностороннем треугольнике:

Ординату $y_3$ найдем, учитывая, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, имеем:

Вычислим ординату центра тяжести:

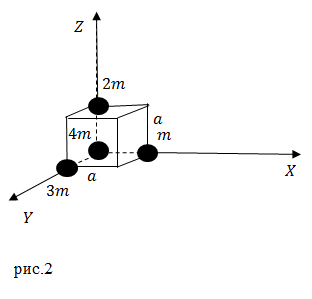
Задание: Каковы координаты центра тяжести системы из четырех элементарных масс, расположенных в вершинах куба со стороной равной $a$ (рис.2)?

Решение: Координату $x_c$ центра тяжести найдем как:

Ординату центра тяжести вычислим как:

Для координаты $z_c$ получаем:

Ответ: ($x_y_c,\ z_c$)=($\ 0,1\ a$, $0,3a$, $0,2a$)(м)

Источник статьи: http://www.webmath.ru/poleznoe/fizika/fizika_98_centr_tjazhesti_tela.php