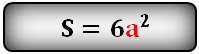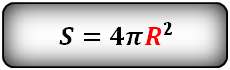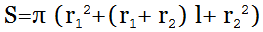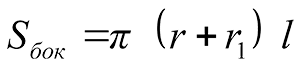- Нахождение площади поверхности усеченного конуса: формулы
- Формулы вычисления площади усеченного конуса
- 1. Боковая поверхность
- 2. Основания
- 3. Полная площадь
- Пример задачи
- Площадь боковой поверхности усеченной пирамиды
- Все формулы для площадей полной и боковой поверхности тел
- 1. Площадь полной поверхности куба
- 2. Найти площадь поверхности прямоугольного параллелепипеда
- 3. Найти площадь поверхности шара, сферы
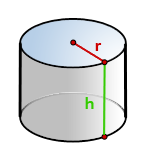
- 4. Найти площадь боковой и полной поверхности цилиндра
- 5. Площадь поверхности прямого, кругового конуса
- Площадь поверхности усеченного конуса
- Расчет площади полной поверхности усеченного конуса
- Усеченный конус. Площадь поверхности усеченного конуса
Нахождение площади поверхности усеченного конуса: формулы
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.
Формулы вычисления площади усеченного конуса
Примечание: иногда усеченный конус, также, называют коническим слоем.
1. Боковая поверхность
Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.
Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.
2. Основания
Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:
Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.
3. Полная площадь
Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.
Sполн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2 )
Пример задачи
Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.
Решение
Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.
Sбок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см 2
Sосн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см 2
Sосн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см 2
Sполн. = 427,04 см 2 + 379,94 см 2 + 113,04 см 2 =
Источник статьи: http://microexcel.ru/ploshad-usechennogo-konusa/
Площадь боковой поверхности усеченной пирамиды
Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания: 
Таким же образом находим периметр меньшего основания: 
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу: 
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания: 

Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Источник статьи: http://2mb.ru/matematika/geometriya/ploshhad-bokovoj-poverxnosti-usechennoj-piramidy/
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба
a — сторона куба
Формула площади поверхности куба,(S):
2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
3. Найти площадь поверхности шара, сферы
R — радиус сферы
Формула площади поверхности шара (S):
4. Найти площадь боковой и полной поверхности цилиндра
r — радиус основания
h — высота цилиндра
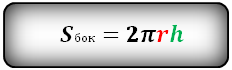
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
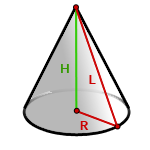
5. Площадь поверхности прямого, кругового конуса
R — радиус основания конуса
H — высота
L — образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Источник статьи: http://www-formula.ru/2011-09-24-00-29-48
Площадь поверхности усеченного конуса
Если в объемной геометрической фигуре, представляющей конус, провести сечение параллельно его основанию, то получится усеченный конус. Верхнее и нижнее основания данного конуса имеют форму круга. Чтобы определить площадь усеченного конуса, следует определить S боковой поверхности, а также площади нижнего и верхнего основания, после чего эти величины суммируются. При проектировании различных сооружений и строительных конструкций очень часто используется такой важный элемент, как усеченный конус. Зная S усеченного конуса, конструктору проще определиться с материалом для инженерных конструкций и и их показателями прочности.
S боковой поверхности рассчитывается по формуле:
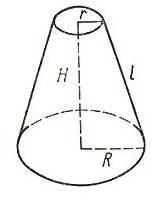
В данной формуле:
r1 — длина радиуса нижнего основания;
r2 — длина радиуса верхнего основания;
l — величина образующей.
Рассчитать площадь усеченного конуса можно с помощью онлайн калькулятора. Это значительно сэкономит вам время.
Расчет площади полной поверхности усеченного конуса
Полная площадь рассчитывается, как сумма площадей двух оснований усеченного конуса и его боковой поверхности по формуле:
где l — величина образующей;
π — величина постоянная, 3,1415;
r1 — длина радиуса нижнего основания;
r2 — длина радиуса верхнего основания.
Источник статьи: http://infofaq.ru/ploshhad-poverxnosti-usechennogo-konusa.html
Усеченный конус. Площадь поверхности усеченного конуса
Разделы: Математика
Тема урока: «Усеченный конус. Площадь поверхности усеченного конуса».
Цели:
обучающая — рассмотреть виды сечений конуса различными плоскостями, ввести понятие усеченного конуса, его элементов, рассмотреть усеченный конус как тело вращения, вывести формулу для вычисления площади боковой и полной поверхности усеченного конуса, показать связь темы с окружающим миром;
развивающая — развивать логическое мышление и конструктивные навыки, сознательное восприятие учебного материала, зрительную память и грамотную математическую речь, навыки самоконтроля и самооценки;
воспитательная — воспитывать познавательную активность, чувство прекрасного, культуру речи и общения, аккуратность.
Методы: информационно – иллюстративный; проблемный диалог; самостоятельная работа, элементы информационных технологий.
Оборудование: компьютер, проектор, записи на доске, раздаточный материал (карточки с заданиями).
План урока:
1. Организационный момент.(1 мин)
2. Историческая справка.(1 мин)
3. Повторение основных сведений о конусе.(5 мин)
4. Объяснение нового материала. (8 мин)
5. Решение задач по готовым чертежам, на нахождение площади
поверхности усеченного конуса (4 задачи).(25 мин)
6. Дополнительная информация о конусе. (3 мин)
7. Задание на дом .(1 мин)
8. Подведение итогов. (1 мин)
Ход урока
Урок сопровождается презентацией. (Приложение)
1. Организационный момент. (Слайд № 1)
Фотография соснового леса. Какое отношение эта фотография имеет к нашему уроку?
Подсказка: С какой фигурой вращения мы познакомились на прошлом уроке? Конус! Конус в переводе с греческого «konos» означает «сосновая шишка».
2. Историческая справка
С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н. э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470–380 гг. до н. э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Платон был учеником Сократа (470–399 гг. до н. э.). Он в 387 г. до н. э. основал в Афинах Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н. э.) – учеником Евклида (III в. до н. э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
3. Повторение основных сведений о конусе
На прошлом уроке мы успели познакомиться с понятием конуса и вывести формулы для нахождения площади боковой и полной поверхности конуса.
Два человека вызываются к доске, решать задачи по карточкам.
Центральный угол в развертке боковой поверхности конуса равен 120°. Площадь боковой поверхности конуса равна 12
Через вершину конуса проведено сечение наибольшей площади. Центральный угол в развертке боковой поверхности конуса равен 270°. Найдите угол между плоскостью сечения и плоскостью основания.
Остальные ребята из класса работают устно. (Слайд № 2)
Что называется конусом? Назовите все элементы конуса.
— образующая конуса больше его высоты?
— существует параллельный перенос, при котором одна из образующих конуса отображается на другую?
Назовите формулу для вычисления площади боковой поверхности конуса. Что является разверткой конуса? Что называется осевым сечением конуса? (Слайд № 3)
— площадь боковой поверхности конуса равняться площади его осевого сечения?
— развертка боковой поверхности конуса быть кругом?
— площадь боковой поверхности конуса равняться площади его основания?
Конус является фигурой вращения. Как можно получить конус? (Слайд № 4)
3. Назовите плоскую фигуру, при вращении которой вокруг одной из сторон образуются два равных конуса с общим основанием.
Проверка ответов учеников, работающих по карточкам.
Определение и формулы повторили, а теперь рассмотрим виды сечений конуса различными плоскостями. (Слайд № 5-7)
4. Объяснение нового материала. (Слайд № 8-15)
Объяснение нового материала проводится с помощью постановки проблемных вопросов так, что выводы делают сами дети.
Усеченным конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной к оси конуса.
Основание данного конуса и круг, полученный в сечении этого конуса плоскостью а, называются основаниями усеченного конуса.
Отрезок, соединяющий центры оснований усеченного конуса, называется его высотой или осью.
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, расположенные между основаниями усеченного конуса, называются его образующими.
Все образующие усеченного конуса равны между собой. Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Осевое сечение усеченного конуса – равнобедренная трапеция.
5. Решение задач на нахождение площади поверхности усеченного конуса (3 задачи)
1. Найдите, чему равна площадь осевого сечения и площадь боковой поверхности усеченного конуса, если радиусы его оснований 3 и 6 см, а высота равна 4 см.
2. Найдите, чему равна осевого сечения и полной поверхности усеченного конуса, образующая равна 30 см, а диагональ осевого сечения равная 40 см перпендикулярна с образующей.
3. Радиусы оснований усеченного конуса равны 16 см и 25 см. Найдите площадь полной поверхности конуса, если в его осевое сечение можно вписать окружность.
Самостоятельная работа с последующей самопроверкой. (Слайд № 19, 20)
1. Найдите ошибочную фразу
- усеченным конусом называется часть конуса, ограниченная его основанием и сечением, плоскость которого параллельна плоскости основания;
- усеченным конусом называется фигура (тело), полученная при вращении равнобедренной трапеции около своей оси;
- усеченным конусом называется фигура, любое осевое сечение которой – равнобедренная трапеция.
2. Длины окружностей оснований усеченного конуса равны 4 

3. Образующая усеченного конуса равна l и составляет с плоскостью основания угол 
6. Дополнительная информация о конусе
1. В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
2. В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
3. «Конусами» называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи.
Раковины используются как украшения, сувениры.
4. По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.
5. В физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает. Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.
7. Задание на дом
П. 55,56 повторить, п. 57
№ 569, 571
На пять: Через середину высоты конуса проведена плоскость, параллельная основанию. Площади полных поверхностей частей конуса, которые при этом образовались, относятся как 3:11. Найдите угол между образующей конуса и плоскостью основания.
8. Подведение итогов
Учитель ещё раз подчёркивает связь математики с окружающим миром и необходимость математических знаний в положительном преобразовании окружающего мира. (Слайды № 26-30)
Источник статьи: http://urok.1sept.ru/articles/538599