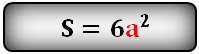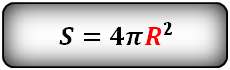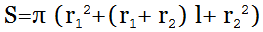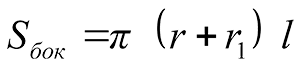Площадь полной поверхности ус

Нахождение площади поверхности усеченного конуса: формулы

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.

Формулы вычисления площади усеченного конуса

Примечание: иногда усеченный конус, также, называют коническим слоем.

1. Боковая поверхность

Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.

Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.

2. Основания

Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:

Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.

3. Полная площадь

Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.

S_полн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2 )

Пример задачи

Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.

Решение

Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.

S_бок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см 2

S_осн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см 2

S_осн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см 2

S_полн. = 427,04 см 2 + 379,94 см 2 + 113,04 см 2 =

Источник статьи: http://microexcel.ru/ploshad-usechennogo-konusa/

Все формулы для площадей полной и боковой поверхности тел

1. Площадь полной поверхности куба

a — сторона куба

Формула площади поверхности куба,(S):

2. Найти площадь поверхности прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R — радиус сферы

Формула площади поверхности шара (S):

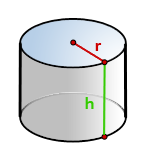
4. Найти площадь боковой и полной поверхности цилиндра

r — радиус основания

h — высота цилиндра

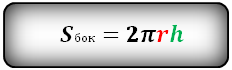
Формула площади боковой поверхности цилиндра, (S _бок ):

Формула площади всей поверхности цилиндра, (S):

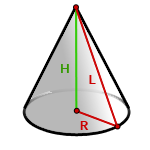
5. Площадь поверхности прямого, кругового конуса

R — радиус основания конуса

H — высота

L — образующая конуса

Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S _бок ):

Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S _бок ):

Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):

Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):

Источник статьи: http://www-formula.ru/2011-09-24-00-29-48

Площадь поверхности усеченного конуса

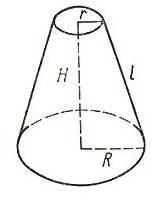
Если в объемной геометрической фигуре, представляющей конус, провести сечение параллельно его основанию, то получится усеченный конус. Верхнее и нижнее основания данного конуса имеют форму круга. Чтобы определить площадь усеченного конуса, следует определить S боковой поверхности, а также площади нижнего и верхнего основания, после чего эти величины суммируются. При проектировании различных сооружений и строительных конструкций очень часто используется такой важный элемент, как усеченный конус. Зная S усеченного конуса, конструктору проще определиться с материалом для инженерных конструкций и и их показателями прочности.
S боковой поверхности рассчитывается по формуле:

В данной формуле:
r1 — длина радиуса нижнего основания;
r2 — длина радиуса верхнего основания;
l — величина образующей.

Рассчитать площадь усеченного конуса можно с помощью онлайн калькулятора. Это значительно сэкономит вам время.

Расчет площади полной поверхности усеченного конуса

Полная площадь рассчитывается, как сумма площадей двух оснований усеченного конуса и его боковой поверхности по формуле:

где l — величина образующей;
π — величина постоянная, 3,1415;
r1 — длина радиуса нижнего основания;
r2 — длина радиуса верхнего основания.

Источник статьи: http://infofaq.ru/ploshhad-poverxnosti-usechennogo-konusa.html

Калькулятор онлайн расчета площади полной и боковой поверхности усеченного конуса с отображением формул и подробным решением.

Калькулятора онлайн рассчитывает площадь боковой и полной поверхности усеченного конуса и выводит формулы с подробным решением:

• площадь боковой S_side поверхности усеченного конуса равна произведению π, образующей и суммы нижнего и верхнего радиусов оснований.
• площадь полной S_full поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и его оснований. Основания усеченного конуса есть круги и их площадь вычисляется по формуле площади круга.

площадь полной поверхности:

расчет площади полной поверхности усеченного конуса

площадь боковой поверхности:

расчет площади боковой поверхности усеченного конуса

расчет площади боковой поверхности усеченного конуса

Исходные данные:			Решение:
Образующая усеченного конуса	L =
Радиус нижнего основания	R =
Радиус верхнего основания	r =

I. Для справки:

1. Усеченный конус — тело ограниченное сечением, параллельным основанию, и боковой поверхностью конуса.

2. Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

3. Площадь поверхности — аддитивная числовая характеристика поверхности.

Источник статьи: http://www.premierdevelopment.ru/ploshhad-poverhnosti-usechennogo-konusa.html

Площадь полной поверхности ус

Ниже вы узнаете, по какой формуле рассчитывается площадь боковой и полной поверхности усеченного конуса, а также сможете рассчитать обе площади онлайн.

Обычно конусом называют именно прямой круговой конус. Площади боковой и полной поверхности такого конуса рассчитывают через радиусы его сечения и оснований.

С помощью следующего калькулятора вы сможете рассчитать площадь боковой поверхности конуса.

Площадь боковой поверхности усечённого конуса

Для расчёта боковой поверхности конуса пользуются формулой:

$S_ <бок>= π \cdot (R_1 + R_2) \cdot l$, где

$R_1, R_2$ — радиусы основания и сечения конуса;

$l$ — образующая конуса;

Чтобы разобраться, как использовать эту формулу, рассмотрим пример.

Задача

Рассчитайте площадь боковой поверхности усечённого конуса, радиус основания $R_1$ которого равен $7$ см, радиус сечения $R_2$ равен $4$ см, а длина образующей $l$ равна также $7$ см.

Решение:

$S_ <бок>= 3.14 \cdot (7 + 4) \cdot 7 = 241.9$ см$^2$.

Ответ совпадает с решением онлайн-калькулятора, а значит, он — правильный.

Готовые работы на аналогичную тему

Для нахождения площади полной поверхности усечённого конуса нужно сложить площади его основания, сечения и боковой поверхности.

Это можно сделать с помощью нижеприведённого онлайн-калькулятора.

Площадь полной поверхности усечённого конуса

Полную площадь поверхности усечённого конуса рассчитывают по формуле:

$S = π \cdot (R_1 + R_2) \cdot l + S_1 + S_2 \left(1\right)$, где

$R_1, R_2$ — радиусы основания конуса и его сечения;

$l$ — длина образующей конуса;

$S_1, S_2$ — площади основания и сечения конуса.

Подставив в формулу $(1)$ площади основания и сечения, получим:

$S = π \cdot (R_1 + R_2) \cdot l + π \cdot R_1^2 + π \cdot R_2^2$.

На примере усечённого конуса из предыдущей задачи рассчитаем полную площадь поверхности.

Задача

Чему равна площадь полной поверхности конуса с $R_1 = 7$, $R_2 = 4$ и образующей $l = 7$?

Решение:

Площадь полной поверхности складывается из площадей основания, сечения и боковой поверхности. Боковую поверхность мы нашли в предыдущем примере, следовательно:

$S_ <полн>= 241.9 + 3.14 \cdot 7^2 + 3.14 \cdot 4^2 = 241.90 + 153.94 + 50.27 = 446.10$ см$^2$.

Ответ совпадает с ответом, рассчитанным онлайн, а значит, решение верное.

Источник статьи: http://spravochnick.ru/calculators/ploschad_usechennogo_konusa/