Признаки равенства треугольников сус усу ссс

Можете объяснить что такое СУС , УСУ , ССС в геометрии.Дам 80 баллов!

Ответ:

СУС-теорема» — это признак равенства треугольников по двум сторонам и углу между ними.

УСУ — Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

ССС — если три стороны одного треугольника соостветственно ровны трём сторонам другого треугольника, то эти треугольники равны

1. Всего частей: 3+5+10 = 18, в одной части: 360° : 18 = 20°

2. Тогда:

1) дуга AC = 3*20° = 60°

2) дуга BC = 5*20° = 100°

3) дуга AB = 10*20° = 200°

3. Углы ВАС, АСВ и АВС — вписанные в окружность, они равны половиине центральных углов, а т.к. центральные углы равны градусной мере дуг, то вписанные углы равны половине градусной мере дуги:

1) угол ВАС = 0,5 дуги ВС = 50°

2) угол ВСА = 0,5 дуги АВ = 100°

3) угол АВС = 0,5 дуги АС = 30°

из этих углов меньший угол — угол АВС = 30°

Источник статьи: http://otvet.ws/questions/3397550-mozhete-obyasnit-chto-takoe-sus-usu-sss-v-geometrii-dam-80-ballov.html

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

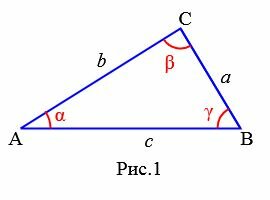Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

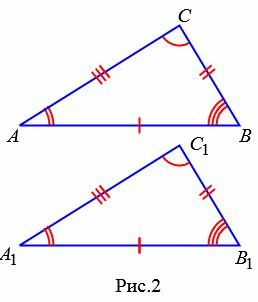
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

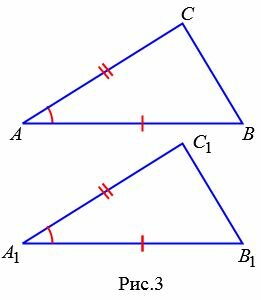Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

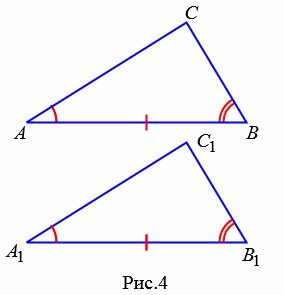Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

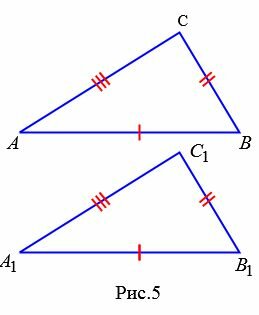Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

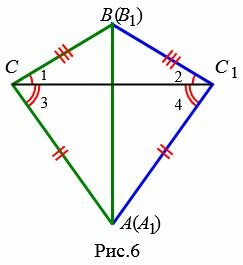Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

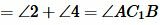Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

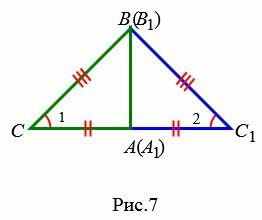Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

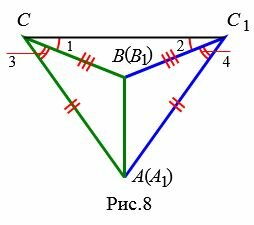Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

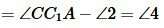Имеем AC=A₁C₁, BC=B₁C₁ и по первому признаку равенства треугольников . Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

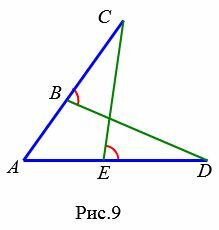Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

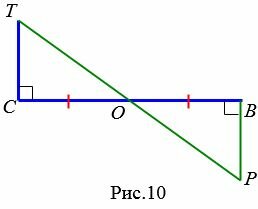Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Источник статьи: http://matworld.ru/geometry/treugolniki.php

Презентация по математике на тему «Признаки равенства треугольников»

Описание презентации по отдельным слайдам:

Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) — древнеегипетское учебное руководство по арифметике и геометрии

Герон Александрийский (вероятно, I-II вв. н. э.)-древнегреческий инженер, физик, механик, математик, изобретатель.

Прямоугольный треугольник применялся тысячелетия назад строителями египетских пирамид. С В

Для составления красивых паркетов часто использовали треугольники.

Треугольники в конструкции мостов.

Высоковольтные линии электропередачи. Треугольники делают конструкции надежными.

Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.

Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.

При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника», основанное на психологии покупателя.

В художественной литературе, телесериалах сюжет часто завязан на «любовном треугольнике».

Сумма длин трех сторон треугольника называется …….. Две фигуры называют равными, если их можно…………. наложением Если два треугольника равны, то элементы одного треугольника ……………….равны элементам другого треугольника В равных треугольниках против соответственно равных сторон лежат равные……… Сумма смежных углов равна………о Если сторона и два ………… к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Утверждение ………………..которого устанавливается путем рассуждений, называется теоремой Если две стороны и………между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны Теоретический тест:

8 баллов – «5» 7-6 баллов – «4» 4-5 баллов – «3» Переведите полученные баллы в отметку : Периметр Совместить Соответственно Углы 180 Прилежащих Справедливость Угол

Признаки равенства треугольников:

Решение задач по готовым чертежам:

Решение задач по готовым чертежам:

Решение задач по готовым чертежам:

Проверка I признак II признак III признак 2 1 3 D М А В С Не учишь! ВЕРНО! 1

A M K B 1 2 3 I признак II признак III признак Не верно! Проверка ВЕРНО! 2

Проверка I признак II признак III признак 1 2 3 D М А В С Не учишь! ВЕРНО! 3

Проверка Не верно! 1 2 3 I признак II признак III признак A В К С ВЕРНО! 4

Не верно! Проверка I признак II признак III признак 1 2 3 ВЕРНО! B С О М 5

О применении признаков равенства треугольников

№1.При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500 м. Верно ли сделан вывод? Докажите.

Для нахождения расстояния от точки В до дерева А на другой стороне реки отметили на местности точки C, D и F так, чтобы точка С была серединой отрезка BD и угол BDF был бы равен углу АВС. Наметив прямую AF, проходящую через точку С, измерили одну из сторон треугольника FDC и приняли ее длину за расстояние АВ. Какую сторону измерили? Докажите предположение.

«Геометрия- это витамин для мозга»

Четыре страны имеют форму треугольников. Нарисуйте, как расположены друг относительно друга страны, если у каждой из них есть общие границы с двумя другими

Продолжи предложение: Сегодня на уроке я узнал… я научился… я повторил… я закрепил…

Номер материала: ДБ-244503

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник статьи: http://infourok.ru/prezentaciya-po-matematike-na-temu-priznaki-ravenstva-treugolnikov-1244774.html