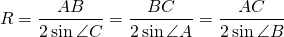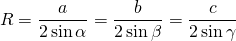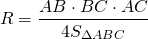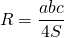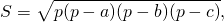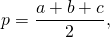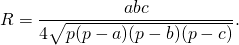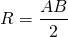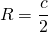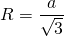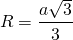Ра ди ус опи сан ной около этого тре уголь ни ка окружности

Радиус описанной около треугольника окружности

Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.

Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.

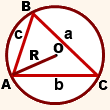
Радиус описанной около произвольного треугольника окружности

То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.

В общем виде эту формулу записывают так:

То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.

Если площадь треугольника находить по формуле Герона

где p — полупериметр,

то получим формулу радиуса описанной около треугольника окружности через длины сторон:

Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.

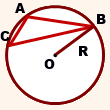
Радиус окружности, описанной около прямоугольного треугольника

Формула:

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:

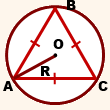
Радиус окружности, описанной около правильного треугольника

Если без иррациональности в знаменателе, то

В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:

Источник статьи: http://www.treugolniki.ru/radius-opisannoj-okolo-treugolnika-okruzhnosti/

Ра ди ус опи сан ной около этого тре уголь ни ка окружности

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Построим OA и OC радиусы. Центральный угол AOC равен 360°:8 = 45°. Угол ABC — вписанный и опирается на ту же дугу, поэтому он равен 45°:2 = 22,5°.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Угол ABC — вписанный и опирается на диаметр AC. Таким образом, ∠ABC = 90°.

Аналоги к заданию № 311503: 311507 Все

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Воспользуемся теоремой косинусов:

(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.

Диаметр описанной окружности найдем по обобщенной теореме синусов:

Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:

Приведем решение Андрея Ларионова.

Угол при основании равен

Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.

Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.

Источник статьи: http://oge.sdamgia.ru/test?theme=36

Ра ди ус опи сан ной около этого тре уголь ни ка окружности

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны 60°. Тогда

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны по 60°. Тогда

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Это задание ещё не решено, приводим решение прототипа.

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны 60°. Тогда

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Это задание ещё не решено, приводим решение прототипа.

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны 60°. Тогда

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Это задание ещё не решено, приводим решение прототипа.

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны 60°. Тогда

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Это задание ещё не решено, приводим решение прототипа.

Сторона правильного треугольника равна Найдите радиус окружности, описанной около этого треугольника.

Треугольник ABC правильный, значит, все его углы равны 60°. Тогда

Источник статьи: http://ege.sdamgia.ru/test?likes=27892

Подготовительная работа по математике (Задание №26: Комбинация многоугольников и окружностей) для ОГЭ (ГИА) от Решу ОГЭ в 2019 году

Просмотр

ответы 1)4,5 2)168 3)45 — 5)45 6)52 7)24 8)10 9)4,8 10)14 12)161,5 13)3 14)24;104;52 15)26 16)50 18)5,4 19)15 20)9 21)25 22)17

Ответы

Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Решения

Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Статистика и загрузка

Скачать

Сервера

Просмотров	351	102	Загрузок
Добавил	Гость	24.11.2019	Дата
День	Воскресенье	23:51	Время

Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.

Все материалы сайта представлены исключительно в ознакомительных целях.

Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.

Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.

Источник статьи: http://yagubov.ru/math/40-1-0-17378