Стебель с листьями ящик с усами

Создание блочной диаграммы с ограничителями выбросов

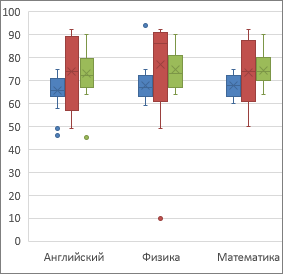
Диаграмма «ящик с усами» показывает распределение данных по квартилям, выделяя их выбросы. В полях могут быть линии, протянутые вертикально под названием «усы». Эти линии указывают на отклонение за пределами верхнего и нижнего квартилей, и любая точка за пределами этих линий (усов) считается выбросом.

Диаграмма «ящик с усами» чаще всего используется в статистическом анализе. Например, с помощью нее можно сравнить результаты медицинских испытаний или экзаменационные баллы учащихся.

Создание диаграммы «ящик с усами»

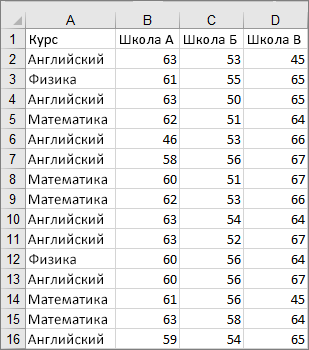
Выделите данные (один или несколько рядов).

Значения на изображении ниже являются частью набора данных, на основе которого был создан показанный выше образец диаграммы.

В Excel выберите команды Вставка > Вставить диаграмму статистики > Ящик с усами, как показано на рисунке ниже.

Важно: В Word, Outlook и PowerPoint порядок действий немного другой.

На вкладке Вставка в группе Иллюстрации нажмите кнопку Диаграмма.

В диалоговом окне Вставка диаграммы на вкладке Все диаграммы выберите элемент Ящик с усами.

На вкладках Конструктор и Формат можно настроить внешний вид диаграммы.

Если они не отображаются, щелкните в любом месте диаграммы «ящик с усами», чтобы добавить на ленту область Работа с диаграммами.

Параметры диаграммы «ящик с усами»

Щелкните правой кнопкой мыши одно из полей на диаграмме, чтобы выбрать его, а затем в контекстном меню выберите пункт Формат ряда данных.

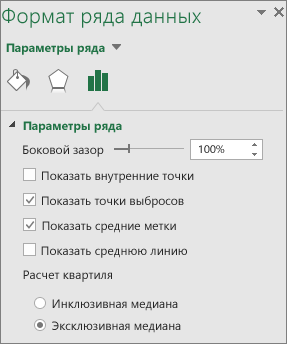
В области Формат ряда данных, выбрав Параметры ряда, внесите необходимые изменения.

(Руководствуйтесь информацией в таблице под приведенным ниже рисунком.)

Управление зазором между категориями.

Показывать внутренние точки

Отображение точек данных между верхней и нижней усами. .

Показывать точки выбросов

Отображает точки выбросов, которые находятся ниже линии верхней или нижней точки уса. .

Показывать маркеры медиан

Отображение маркеров медианы выбранного ряда.

Показывать линию медиан

Отображение линии, соединяющей медианы блоков в выбранном ряде.

Выберите метод вычисления медиан.

Инклюзивная медиана Медиана включается в вычисления, если N (число значений в данных) — нечетное число.

Исключающая медиана Медиана исключается из вычислений, если N (число значений в данных) — нечетное число.

Совет: Дополнительные сведения о диаграммах «ящик с усами», а также их пользе для визуализации статистических данных см. в этой записи о гисторамме, диаграммах Парето и «ящик с усами» блога группы разработчиков Excel. Дополнительные сведения о других новых типах диаграмм приведены в этой записи блога.

Создание диаграммы «ящик с усами»

Выделите данные (один или несколько рядов).

Значения на изображении ниже являются частью набора данных, на основе которого был создан показанный выше образец диаграммы.

На ленте на вкладке «Вставка» щелкните (значок статистической диаграммы) и выберите «Ящик с усами».

На вкладке «Конструктор диаграмм» и «Формат» можно настроить внешний вид диаграммы.

Если вкладки «Конструктор диаграмм» и «Формат» не вы видите, щелкните в любом месте диаграммы «ящик с усами», чтобы добавить их на ленту.

Параметры диаграммы «ящик с усами»

Щелкните одно из полей на диаграмме, чтобы выбрать его, а затем на ленте нажмите кнопку «Формат».

Внести нужные изменения можно с помощью инструментов на вкладке «Формат».

Источник статьи: http://support.microsoft.com/ru-ru/office/%D1%81%D0%BE%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-%D0%B1%D0%BB%D0%BE%D1%87%D0%BD%D0%BE%D0%B9-%D0%B4%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D1%8B-%D1%81-%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%B8%D1%82%D0%B5%D0%BB%D1%8F%D0%BC%D0%B8-%D0%B2%D1%8B%D0%B1%D1%80%D0%BE%D1%81%D0%BE%D0%B2-62f4219f-db4b-4754-aca8-4743f6190f0d

Визуализация статистических данных с помощью диаграммы ящик с усами

Предыстория. В связи с холодными днями в мае и июне 2017 г. я изучил климатические данные многолетних наблюдений, и хотел опубликовать заметку о статистическом взгляде на всё это безобразие. В качестве иллюстрации одной из своих идей я построил блочную диаграмму. Во время ее форматирования я обнаружил, что не вполне понимаю, по каким алгоритмам Excel рисует на ней границы квартилей. Углубившись в вопрос, я узнал много нового, о чем захотел поделиться с читателями блога. Но подумал, что описание тонких алгоритмов как бы повисает в воздухе, и поэтому решил начать с небольшого теоретического введения.

Рис. 1. Визуальное представление выборки: (а) диаграмма разброса показывает все элементы выборки; (б) 5-числовая сводка в виде графика ящик с усами

Скачать заметку в формате Word или pdf, примеры в формате Excel

5-числовая сводка данных

Изучая выборку, мы можем визуализировать все ее значения (рис. 1а), а можем научиться выражать в сжатом виде наиболее часто встречающиеся общие особенности. В последнем случае используют сводки данных. Сегодня наиболее популярными сводками (или статистиками) являются среднее значение и среднеквадратичное отклонение (подробнее см. Определение среднего значения, вариации и формы распределения. Описательные статистики). Однако, во-первых, так было не всегда, а во-вторых, не во всех случаях эти статистики лучше всего описывают выборку.

Любопытный пример приводит Нассим Николас Талеб (см. Черный лебедь. Под знаком непредсказуемости). Если вы определяете средний рост 100 человек, то нахождение среди этой сотни самого высокого человека в мире (2 м 72 см) не сильно изменит среднее значение. А вот если вы определяете среднее богатство 100 человек, то наличие среди них Билла Гейтса ($86,8 млрд.) полностью исказит картину. В этих случаях более релевантной сводкой является медиана.

Медиана – такое число, что ровно половина из элементов выборки больше него, а другая половина меньше него. Если случайные данные упорядочить по возрастанию, получится вариационный ряд. Если такой ряд содержит нечетное число элементов, то медиана – среднее из них; если четное, то медиана – половина суммы двух средних элементов.

В своей, уже ставшей классической, работе Анализ результатов наблюдений. Разведочный анализ Джон Тьюки предлагает 5-числовые сводки, которые включают: минимальное значение, первый квартиль, медиану, третий квартиль, максимальное значение. Процесс нахождения медианы, а затем квартилей можно представить себе, как складывание листа бумаги. Поэтому эти новые значения Тьюки называет сгибами (подробнее см. КВАРТИЛЬ: какие формулы расчета использует Excel). Чтобы представить 5-чиловую сводку визуально, Тьюки предлагает построить график ящик с усами (рис. 1б).

Диаграмма ящик с усами в Excel 2016

В предыдущих версиях Excel приходилось шаманить, чтобы представить статистические данные (см., например, Биржевая диаграмма, она же блочная, она же ящичная). В качестве альтернативы я иногда использовал R (см. Алексей Шипунов. Наглядная статистика. Используем R!). Сейчас же визуализация статистических данных выполняется в несколько кликов. Очень удобно! Вот только Microsoft почему-то сделал весьма краткое описание того, что же собственно отражают элементы диаграммы ящик с усами (см. поддержку MS). Восполним же этот пробел))

Построим диаграмму ящик с усами на основе данных о средних температурах июля за последние 30 лет (рис. 2).

Рис. 2. Основные настройки диаграммы ящик с усами

На рисунке под диаграммой рассчитана 5-числовая сводка. На диаграмме:

• нижний ус соответствует минимальному значению в выборке данных,
• низ ящика – 1-му квартилю,
• линия внутри ящика – медиане,
• верх ящика – 3-му квартилю,
• верхний ус – второму максимальному значению (выбросы не учитываются); если бы данные не содержали выброса, верхний ус соответствовал бы максимальному значению,
• опциально отдельными точками показаны выбросы.

Рассмотрим параметры ряда подробнее (см. Формат ряда данных на правой части рис. 2). Боковой зазор определяет ширину ящика и ширину горизонтальных границ усов, а также расстояние между ящиками, если их несколько (рис. 3). Параметр Показать внутренние точки – говорит сам за себя (рис. 4). Показать точки выбросов – любопытно, что Excel просто перестает показывать выбросы, при этом никак не меняет параметры ящика и усов (рис. 5). Показать средние метки – наряду с медианной линией отражает в виде крестика среднее арифметическое значение по выборке (рис. 6). Видно, что среднее арифметическое смещено относительно медианы вверх (в сторону выброса). Среднее арифметическое более чувствительно к выбросам по сравнению с медианой. Показать среднюю линию – соединяет средние значения разных категорий. У меня не получилось отразить эти линии. А у Дмитрия Езипова получилось.

Рис. 3. Боковой зазор: слева – 300%, справа – 100%

Рис. 4. Показать внутренние точки; слева параметр выключен, справа – включен

Рис. 5. Показать точки выбросов; слева параметр выключен, справа – включен

Рис. 6. Показать средние метки; слева параметр выключен, справа – включен

Какой метод расчета квартилей предпочесть

И, наконец, самый непонятный параметр форматирования диаграммы ящик с усами – Расчет квартиля. В сообществе статистиков нет единого мнения, по какому алгоритму считать квартили. В Excel используется два алгоритма. Если вы хотите в них досконально разобраться, рекомендую КВАРТИЛЬ: какие формулы расчета использует Excel. Если кратко, то в Excel есть две функции КВАРТИЛЬ.ИСКЛ() и КВАРТИЛЬ.ВКЛ(). Первая использует алгоритм эксклюзивной медианы, вторая – инклюзивной. Алгоритм расчета квартилей в первом случае дает значения чуть более далекие от медианы, т.е. ящик немного более вытянутый. Визуально это не разглядеть, и только если добавить подписи данных, то числа покажут этот эффект (рис. 7).

Рис. 7. Расчет квартиля: (а) эксклюзивная медиана, (б) инклюзивная медиана

Если вы обрабатываете данные в разных программах (Excel, R, SAS…), то для совместимости, наверное, лучше использовать квартили, рассчитанные по методу эксклюзивной медианы. Поскольку этот метод используется во всех продуктах, вы получите одинаковые числа в разных программах. Если же вы работаете только в Excel, я бы рекомендовал метод инклюзивной медианы. Он более чувствителен к выбросам, т.е. при прочих равных КВАРТИЛЬ.ВКЛ() определит точку как выброс при меньшем отклонении от медианы (рис. 8).

Рис. 8. (б) Точка, которая идентифицируется функцией КВАРТИЛЬ.ВКЛ(), как выброс, в то время, как (а) КВАРТИЛЬ.ИСКЛ() еще не считает эту точку выбросом

Источник статьи: http://baguzin.ru/wp/vizualizatsiya-statisticheskih-dannyh/

Диаграмма «ящик с усами» (boxplot) в Excel 2016

Excel 2016, как известно, обогатился новыми типами диаграмм. Одна такая, которая диаграмма Парето, уже была показана. В этот раз рассмотрим другую, чисто статистическую. Называется «ящик с усами» или «коробчатая диаграмма» (box-and-whiskers plot или boxplot).

Раньше я такие видел только в специализированных ПО, типа STATISTICA, и для того, чтобы нарисовать подобную диаграмму в Excel, нужно было изрядно потрудиться. Теперь она есть в стандартном наборе Excel.

Зачем нужна такая диаграмма? Допустим, есть выборка для анализа. А еще лучше несколько выборок, которые нужно сравнить. Для этого рассчитывают различные показатели. Однако к любому расчету всегда хочется добавить наглядности, чтобы мозг перешел в режим образного представления, а не довольствовался сухими цифрами и формулами. Поэтому основные характеристики ловко изображают на рисунке. Отличным вариантом будет как раз диаграмма «ящик с усами».

На рисунке показан формат по умолчанию. Как видно, сравниваются две выборки путем изображения двух «ящиков с усами».

Что здесь что обозначает?

Крестик посередине – это среднее арифметическое по выборке.

Линия чуть выше или ниже крестика – медиана.

Нижняя и верхняя грань прямоугольника (типа ящика) соответствует первому и третьему квартилю (значениям, отделяющим ¼ и ¾ выборки). Расстояние между 1-м и 3-м квартилем – это межквартильный размах (или расстояние).

Горизонтальные черточки на конце «усов» – максимальное и минимальное значение (без учета выбросов, см. ниже).

Отдельные точки – это выбросы, которые показываются по умолчанию. Если значение выходит за пределы 1,5 межквартильных размаха от ближайшего квартиля, то оно считается аномальным. Их можно скрыть (см. ниже настройки).

Во всей красе «ящик с усами» проявляется при сравнении выборок, в которых данные делятся на категории. Допустим, провели некоторый эксперимент среди мужчин и женщин. Есть данные до и после эксперимента по обоим полам. Для анализа потребуется вычислить различные показатели. А если к этому добавить диаграмму «ящик с усами», то результат будет весьма наглядным.

Отлично видно, что после проведения эксперимента данные по мужчинам в целом уменьшились, а данные среди женщин наоборот, увеличились. Это не значит, что выборки больше не нужно анализировать (сравнивать, проверять гипотезы и т.д.). Но наглядность сильно улучшает понимание. Перейдем к настройкам.

Настройки диаграммы «ящик с усами»

Общий вид диаграммы настраивается стандартно. Можно менять цвет, добавлять подписи и т.д. Для этого есть две контекстные вкладки на ленте (Конструктор и Формат). Но есть настройки, предназначенные специально для этой диаграммы.

Выбираем какой-либо ряд и жмем Ctrl+1. Либо два раза кликаем по какому-нибудь «ящику». Можно через правую кнопку Формат ряда данных…. Справа вылазит панель настроек.

Рассмотрим по порядку.

Боковой зазор – регулирует ширину ящиков и расстояние между ними.

Показывать внутренние точки. Если поставить галочку, то на оси, где расположены «усы», точками будут показаны все значения. Так хорошо видно распределение внутри групп.

Показывать точки выбросов – отражать экстремальные значения.

Выбросы – это точки, выходящие за пределы 1,5 межквартильных размаха.

Показать средние метки – среднее арифметическое (крестики). Стоят по умолчанию, но можно скрыть.

Показать среднюю линию – только для различных категорий. Показывает изменения по категориям.

Если добавить линии, то изменения после эксперимента станут видны еще лучше. В справке написано, что соединяются медианы, но на графике почему-то соединяются средние. Чудеса.

Инклюзивная медиана или эксклюзивная медиана. Инклюзивная медиана включает в «ящик» квартильные значения , а эксклюзивная медиана не включает. При выборе «эксклюзивной медианы» верх и низ «ящика» соответствует средней между квартильным и следующим (от центра) значением. По умолчанию стоит «эксклюзивная». Пусть стоит дальше. Причем тут медиана, вообще не понял, – речь ведь про квартиль. Думал, криво перевели, но в английской версии те же названия. В общем, здесь лучше ничего не менять.

Своевременное использование диаграммы «ящик-усы» может дать весьма ценную и наглядную информацию. Аналитику, который использует специализированные программы или трудоемкие настройки Excel, будет очень приятно иметь такую диаграмму под рукой.

Как показано в ролике ниже, все делается очень быстро и просто.

Источник статьи: http://statanaliz.info/excel/diagrammy/diagramma-yashhik-s-usami-boxplot-v-excel-2016/