Усу второй признак треугольника

2 признак равенства треугольников

(Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам)

Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.

Так как AB=A₁B₁, то треугольник A₁B₁C₁ можно наложить на треугольник ABC так, чтобы

• сторона A₁B₁ совместилась со стороной AB,
• точки C₁ и С лежали по одну сторону от прямой AB.

Поскольку ∠A=∠A₁, сторона A₁С₁ при этом наложится на луч AC.

Так как ∠B=∠B₁, сторона B₁C₁ наложится на сторону BC.

Точка С₁ принадлежит как стороне A₁С₁, так и стороне B₁C₁, поэтому С₁ лежит и на луче AC, и на луче CB.

Лучи AC и CB пересекаются в точке C. Следовательно, точка С₁ совместится с точкой C.

Значит, сторона A₁С₁ совместится со стороной AC, а сторона B₁C₁ — со стороной BC.

Таким образом, при наложении треугольники ABC и A₁B₁C₁ полностью совместятся.

Источник статьи: http://www.treugolniki.ru/2-priznak-ravenstva-treugolnikov/

Геометрия. 7 класс

Конспект урока

Второй и третий признаки равенства треугольников

Перечень рассматриваемых вопросов:

• Доказательство и формулировка второго и третьего равенства треугольников.
• Решение задач на доказательство равенства треугольников с использованием признаков.

Теорема ‑ утверждение, справедливость которого устанавливается путём рассуждений в данной системе аксиом.

Второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б.Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т.М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т.М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы.// Иченская М.А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее мы узнали, как определить, являются ли треугольники равными. Для этого мы использовали способ наложения или первый признак равенства треугольников.

Сегодня мы рассмотрим ещё два признака равенства треугольников.

Второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

1. Наложим треугольник ∆ABC на ∆А₁В₁С₁, так чтобы вершина A совместилась с вершиной A₁, вершины B и B₁лежали по одну сторону от A₁C₁.

Так как ∠А =∠А₁, ∠C=∠C₁, то AB наложится на луч A₁B₁, BC наложится на луч B₁C₁ (по аксиоме откладывания угла).

1. Вершина B – с вершиной B₁ (по аксиоме откладывания отрезка).
2. Стороны треугольников BС и B₁С_1, АВ и А₁В₁совместятся (по аксиоме откладывания отрезка).
3. Треугольник ABC и треугольник А₁В₁С₁ полностью совместится →∆АВС = ∆А₁В₁С₁

Третий признак равенства треугольников.

Докажем третий признак равенства треугольников.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

1. Приложим треугольник ∆ ABC к ∆ А₁В₁С₁, так чтобы вершина A совместилась с вершиной A₁, вершина B с B₁, вершины C и C₁лежали по разные стороны от прямой A₁B₁.
2. Так как АC = А₁C₁, BC = B₁C₁(по аксиоме откладывания отрезка), =>∆ А₁C₁С и ∆ В₁С₁C – равнобедренные.
3. ∠1=∠2, ∠3=∠4 (по свойству равнобедренного треугольника) → ∠A₁CB₁ = ∠А₁С₁В₁.

Итак, сегодня мы доказали второй и третий признаки равенства треугольников.

Рассмотрим ещё один случай доказательства третьего признака равенства треугольников.

1. Приложим треугольник ABC к треугольнику А₁В₁С₁, так чтобы вершина A совместилась с вершиной A₁, вершина B с B₁, вершины C и C₁лежали по разные стороны от прямой A₁B₁.
2. Так как АC = А₁C₁,→∆АC₁С – равнобедренный (по определению равнобедренного треугольника. ∠C =∠С₁. (по свойству равнобедренного треугольника).
3. АC = А₁C₁, BC = B₁C₁ (по условию), ∠C = ∠C₁→∆АВС = ∆А₁В₁С₁(по 1 признаку равенства треугольников).

Разбор заданий тренировочного модуля.

№ 1. На рисунке изображены треугольники ABH и BHА₁, ∠1 = ∠2, ∠АВH =∠А₁ВH. Будут ли треугольники ABH и BHА₁ равными?

По условию в треугольниках ABH и BHА₁, ∠1 = ∠2, ∠АВH = ∠А₁ВH, BH ‑ общая сторона.

Следовательно, ∆ABH = ∆BHА₁ (по второму признаку равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.)

№ 2. Периметр треугольника AOR равен 21 см, периметр четырёхугольника AORF равен 22 см. При этом AO = RF, OR = AF. Найти AR.

Для решения задачи, нужно вспомнить формулу периметра треугольника и четырёхугольника.

Р_{∆ AOR} = АО + OR + AR = 21 см

Р_AORF = АО + OR + RF + AF = 22 см

По условию AO = RF, OR = AF, AR ‑ общая сторона →∆AOR = ∆ARF (по 3 признаку равенства треугольников: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны).

Т.к. AO = RF, OR = AF.

Р_AORF = АО + OR + АО + OR = 2 · АО + 2 · OR = 22 см;

Источник статьи: http://resh.edu.ru/subject/lesson/7296/conspect/

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

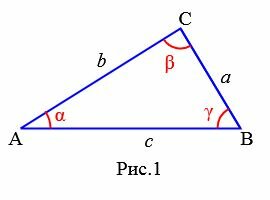Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

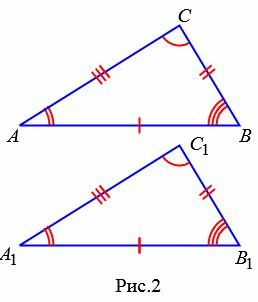
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

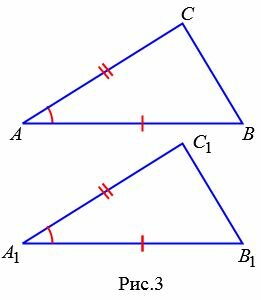Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

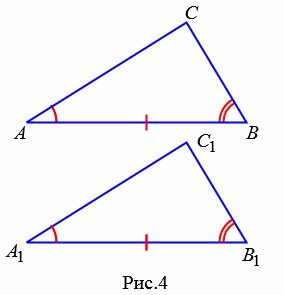Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

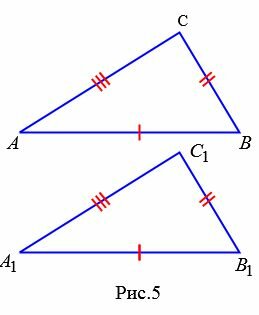Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

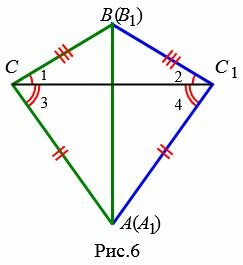Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

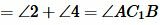Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

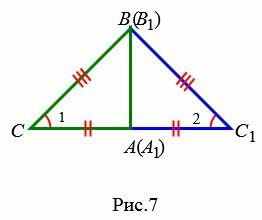Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

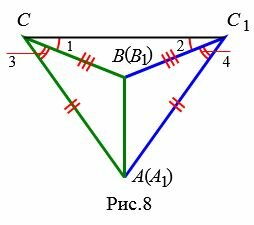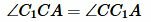
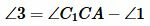Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ и по первому признаку равенства треугольников . Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

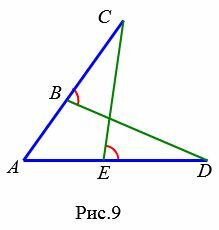Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

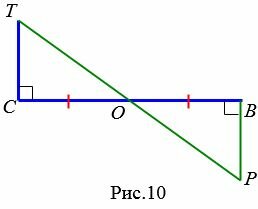Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Источник статьи: http://matworld.ru/geometry/treugolniki.php