Ящик с усами без усов

Ящик с усами

Ящик с усами, диаграмма размаха (англ. box-and-whiskers diagram or plot, box plot ) — график, использующийся в описательной статистике, компактно изображающий одномерное распределение вероятностей.

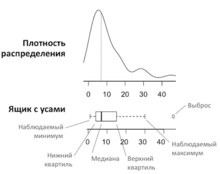
Такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы. Несколько таких ящиков можно нарисовать бок о бок, чтобы визуально сравнивать одно распределение с другим; их можно располагать как горизонтально, так и вертикально. Расстояния между различными частями ящика позволяют определить степень разброса (дисперсии) и асимметрии данных и выявить выбросы.

Содержание

Компактность представления информации

График «ящик с усами», или «ящичковая диаграмма», был разработан Джоном Тьюки в 1970-х годах. По сути, ящик с усами — это быстрый способ изучения одного или нескольких наборов данных в графическом виде. Этот график может показаться более примитивным, чем, например, гистограммы, но он имеет некоторые преимущества. Он занимает меньше места и поэтому особенно полезен для сравнения распределений между несколькими группами или наборами данных. Кроме того, ящик с усами в своей первоначальной форме прост для построения.

На графике 2 приведены два графических представления распределения одной и той же случайной величины. Сверху показана плотность распределения, а снизу ящик с усами. Видно, что ящик с усами более компактный и по нему легко можно оценить медианы, квантили, дисперсию и асимметрию в данных, а также выявить выбросы. Асимметрию данных можно увидеть не только по медиане, смещённой к какому-либо концу ящика, но и по разной длине усов, выходящих из ящика.

График «ящик с усами» очень прост для понимания и именно поэтому часто используется в различных публикациях для визуализации данных.

Построение

Границами ящика служат первый и третий квартили (25-й и 75-й процентили соответственно), линия в середине ящика — медиана (50-й процентиль). Концы усов — края статистически значимой выборки (без выбросов), и они могут определяться несколькими способами. Наиболее распространённые значения, определяющие длину «усов»:

• Минимальное и максимальное наблюдаемые значения данных по выборке (в этом случае выбросы отсутствуют);
• Разность первого квартиля и полутора межквартильных расстояний; сумма третьего квартиля и полутора межквартильных расстояний. В общем виде эта формула имеет вид

• Среднее арифметическое по выборке ± одно стандартное отклонение; [источник не указан 1684 дня]
• 9-й и 91-й процентили;
• 2-й и 98-й процентили.

Данные, выходящие за границы усов (выбросы), отображаются на графике в виде точек, маленьких кружков или звёздочек. Иногда на графике отмечают среднее арифметическое и его доверительный интервал («зарубка» на ящике). Иногда зарубками обозначают доверительный интервал для медианы.

В связи с тем, что не существует единого общего согласия относительно того, как конкретно строить «ящик с усами», при виде такого графика необходимо искать информацию в сопроводительном тексте относительно того, по каким параметрам ящик с усами строился.

Модификации ящика с усами

Несмотря на свою простоту и удобство, первоначальная форма ящика с усами обладает и некоторыми недостатками. Один из таких существенных недостатков — отсутствие на графике информации о количестве наблюдений по выборке. Действительно, ящик с усами позволяет сравнить медианы, квартили, минимумы и максимумы по различным выборкам, но если мы захотим сделать вывод об общей медиане по всей совокупности выборок, то мы не сможем этого сделать, не прибегая к расчётам на исходных данных. В 1978 году первоначальная форма ящика с усами была модифицирована МакГиллом, Ларсеном и Тьюки. Они предложили учитывать размер выборочной совокупности, рисуя ящики разного размера, а также изобразили на графике доверительный интервал для медиан в виде расходящихся клиньев. Чем больше ящик по размерам, тем больше количество наблюдений в выборке, по которой строился этот ящик. Что касается доверительного интервала, то он представляет собой выемки на каждом из ящиков; в случае, если получившиеся выемки разных ящиков не пересекаются, их медианы статистически значимо различаются.

Иная модификация получила название «histplot» (сокр. от «histogram plot», с англ. — «график-гистограмма»). Теперь на графике отображаются плотности распределения по трём точкам: медиане, первому и третьему квартилю. Соответственно, вместо прямоугольника, «ящик» теперь представляет собой две равнобедренные трапеции, имеющие смежное основание.

Дальнейшее изменение получило название «vaseplot» (с англ. — «график-ваза») из-за визуального сходства «ящика» с вазой. На данном графике производится отображение всех плотностей вероятностей от первого до третьего квартиля. Затемнённые области представляют собой доверительный интервал медианы.

Ссылки

• Frigge, M.; Hoaglin, D. C.; Iglewicz, B. (1989). «Some Implementations of the Boxplot». The American Statistician. 43 (1): 50—54. DOI:10.2307/2685173. JSTOR2685173.
• Benjamini, Y. (1988). «Opening the Box of a Boxplot». The American Statistician. 42 (4): 257—262. DOI:10.2307/2685133. JSTOR2685133.
• Поп-математика для взрослых детей
• Диаграмма размаха

Что такое wiki2.info Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной.

Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License.

Wikipedia® — зарегистрированный товарный знак организации Wikimedia Foundation, Inc. wiki2.info является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation).

Источник статьи: http://wiki2.info/%D0%AF%D1%89%D0%B8%D0%BA_%D1%81_%D1%83%D1%81%D0%B0%D0%BC%D0%B8

Создание блочной диаграммы с ограничителями выбросов

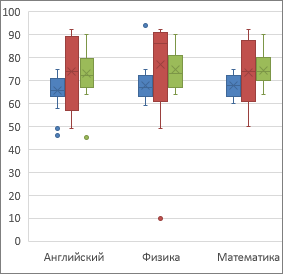
Диаграмма «ящик с усами» показывает распределение данных по квартилям, выделяя их выбросы. В полях могут быть линии, протянутые вертикально под названием «усы». Эти линии указывают на отклонение за пределами верхнего и нижнего квартилей, и любая точка за пределами этих линий (усов) считается выбросом.

Диаграмма «ящик с усами» чаще всего используется в статистическом анализе. Например, с помощью нее можно сравнить результаты медицинских испытаний или экзаменационные баллы учащихся.

Создание диаграммы «ящик с усами»

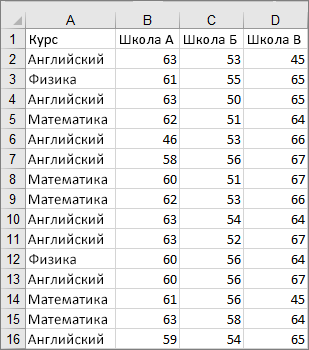
Выделите данные (один или несколько рядов).

Значения на изображении ниже являются частью набора данных, на основе которого был создан показанный выше образец диаграммы.

В Excel выберите команды Вставка > Вставить диаграмму статистики > Ящик с усами, как показано на рисунке ниже.

Важно: В Word, Outlook и PowerPoint порядок действий немного другой.

На вкладке Вставка в группе Иллюстрации нажмите кнопку Диаграмма.

В диалоговом окне Вставка диаграммы на вкладке Все диаграммы выберите элемент Ящик с усами.

На вкладках Конструктор и Формат можно настроить внешний вид диаграммы.

Если они не отображаются, щелкните в любом месте диаграммы «ящик с усами», чтобы добавить на ленту область Работа с диаграммами.

Параметры диаграммы «ящик с усами»

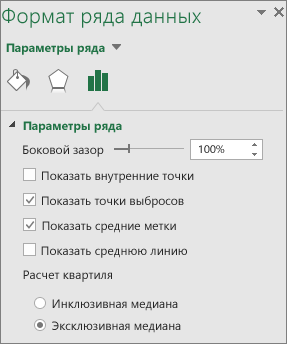
Щелкните правой кнопкой мыши одно из полей на диаграмме, чтобы выбрать его, а затем в контекстном меню выберите пункт Формат ряда данных.

В области Формат ряда данных, выбрав Параметры ряда, внесите необходимые изменения.

(Руководствуйтесь информацией в таблице под приведенным ниже рисунком.)

Управление зазором между категориями.

Показывать внутренние точки

Отображение точек данных между верхней и нижней усами. .

Показывать точки выбросов

Отображает точки выбросов, которые находятся ниже линии верхней или нижней точки уса. .

Показывать маркеры медиан

Отображение маркеров медианы выбранного ряда.

Показывать линию медиан

Отображение линии, соединяющей медианы блоков в выбранном ряде.

Выберите метод вычисления медиан.

Инклюзивная медиана Медиана включается в вычисления, если N (число значений в данных) — нечетное число.

Исключающая медиана Медиана исключается из вычислений, если N (число значений в данных) — нечетное число.

Совет: Дополнительные сведения о диаграммах «ящик с усами», а также их пользе для визуализации статистических данных см. в этой записи о гисторамме, диаграммах Парето и «ящик с усами» блога группы разработчиков Excel. Дополнительные сведения о других новых типах диаграмм приведены в этой записи блога.

Создание диаграммы «ящик с усами»

Выделите данные (один или несколько рядов).

Значения на изображении ниже являются частью набора данных, на основе которого был создан показанный выше образец диаграммы.

На ленте на вкладке «Вставка» щелкните (значок статистической диаграммы) и выберите «Ящик с усами».

На вкладке «Конструктор диаграмм» и «Формат» можно настроить внешний вид диаграммы.

Если вкладки «Конструктор диаграмм» и «Формат» не вы видите, щелкните в любом месте диаграммы «ящик с усами», чтобы добавить их на ленту.

Параметры диаграммы «ящик с усами»

Щелкните одно из полей на диаграмме, чтобы выбрать его, а затем на ленте нажмите кнопку «Формат».

Внести нужные изменения можно с помощью инструментов на вкладке «Формат».

Источник статьи: http://support.microsoft.com/ru-ru/office/%D1%81%D0%BE%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-%D0%B1%D0%BB%D0%BE%D1%87%D0%BD%D0%BE%D0%B9-%D0%B4%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D1%8B-%D1%81-%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%B8%D1%82%D0%B5%D0%BB%D1%8F%D0%BC%D0%B8-%D0%B2%D1%8B%D0%B1%D1%80%D0%BE%D1%81%D0%BE%D0%B2-62f4219f-db4b-4754-aca8-4743f6190f0d

Диаграмма «ящик с усами» в статистике

Содержание:

Диаграмма «ящик с усами»

Построение диаграммы «Ящик с усами» рассмотрим на следующем примере

Задача пример №154

15 работников фирмы при сдаче экзамена по технике безопасности, получили следующие баллы:

13 9 18 15 14 21 7 10 11 20 5 18 37 16 17.

Представьте данную информацию в виде диаграммы «ящик с усами».

Решение:

1. Расположите данные в порядке возрастания, определите медиану и отметьте ее через .

2. Данные слева от медианы расположены в первой нижней половине, справа от медианы — в верхней половине. Т.е. медиана делит данные на две половинки.

3. Медианы половинок, называемые квартилями (здесь = 10, = 18), разбивают данные на 4 части.

4. Определяют изменение между квартилями — = 18 — 10 = 8

5. Отметим на числовой оси наименьшее и наибольшее значения, квартили и медиану — 5 важных точек. Нарисуем прямоугольник, длина которого равна разности изменению между квартилями. Этот прямоугольник делится медианой на две части. Теперь нарисуем «усы», соединив наибольшее и наименьшее значения с соответствующими квартилями.

Мы построили диаграмму «ящик с усами» в соответствии с представленными данными. Теперь, по диаграмме, представим данные. Из диаграммы видно, что приблизительно половина, 50 % , из 15 человек набрали от 10 до 18 баллов, 25% — меньше 10 баллов и 25% — больше 10 баллов.

Разница длин левого и правого «уса» зависит от разницы значений данных в соответствующих частях.

Для построении диаграммы «ящик с усами» из заданной совокупности выделяют 5 значений:

Медиану , квартиль , значение которого меньше медианы и является медианой нижней половины, квартиль , значение которого больше медианы и является медианой верхней половины множества данных, наибольшее и наименьшее значения.

Шаги построения диаграммы «ящик с усами»

1. Проводится горизонтальная прямая.

2. В зависимости от диапазона изменения данных проводится деление.

3. На прямой отмечают 5 значений — , , , наименьшее значение, наибольшее значение.

4. От до рисуется ящик.

5. Рисуем «усы» от : до минимального значения и от до максимального значения.

Задача пример №155

Ниже представлены данные возраста участниц женской паралимпийской команды по волейболу

24, 30, 30, 22, 25, 22, 18, 25, 28, 30, 25, 27. Представьте данные в виде диаграммы «ящик с усами».

Решение:

1. Расположим данные и найдем медиану и квартили.

2. Изобразим числовую ось и отметим эти следующие данные.

3. При помощи разности квартилей — = 29 -23 = 6 нарисуем ящик и разделим его на две части (при помощи медианы). Соединим ящик с наибольшим и наименьшим значением.

4. Представление диаграммы. Возраст 50% баскетболисток между 23-29 годами, 25% меньше 23 лет, 25% — больше 29 лет. Длинными или короткими являются «усы» ящика показывает, близко ли или далеко расположены друг от друга данные внутри 25% — го интервала. Например, левый «ус» длиннее, правый — короче. Так как в 25%-интервале значения изменяются между 18-23, а в левом «усе» мы встречаем только два значения 29-30.

Данные, которые сильно отличаются от основных данных совокупности, называются выбросами. Выбросы можно определить относительно верхнего и нижнего квартиля. В этом случае выбросом считается, значение в 1,5 раза больше или меньше разности — . Например, в рассмотренном нами примере нижний квартиль 23, верхний квартиль 29, разность квартилей 6. Тогда значения 23 — 1,5 • 6 = 14 и 29 + 1,5 • 6 = 38 считаются граничными значениями. Все значения, которые больше 38 и меньше 14, называются выбросами.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник статьи: http://natalibrilenova.ru/diagramma-yaschik-s-usami-v-statistike/