Ящик с усами matplotlib

2. Я новичок. Можно попроще?

Новичкам, которые пытаются изучать matplotlib самостоятельно, рано или поздно, начинает казаться, что все слишком запутано и сложно. Вроде бы все примеры с официального руководства работают, получаются красивые картинки. Но сделать, что-то свое либо не получается, либо получается, но без понимания того, как это работает.

Как с ней познакомиться и с какого края к ней подойти? Библиотека matplotlib предназначена для создания научной графики. На мой взгляд, знакомство лучше начать с двух простых вопросов:

• Какие бывают графики?
• Как они строятся?

Учитывая, что в простейшем случае, графики строятся парой-тройкой строчек кода, вы очень скоро убедитесь в том, что все довольно просто.

2.1. График линии

Метод построения линии очень прост:

• есть массив абсцис ( x );
• есть массив ординат ( y );
• элементы с одинаковым индексом в этих массивах — это координаты точек на плоскости;
• последовательные точки соединяются линией.

Под массивами, подразумеваются списки, кортежи или массивы NumPy. Кстати, последние предоставляют гораздо больше удобств чем списки и кортежи, поэтому знание пакета NumPy может значительно упростить вам жизнь.

Давайте выполним следующий код:

В результате мы получим вот такой простой график:

Метод plt.plot() , в простейшем случае, принимает один аргумент — последовательность чисел, которая соответствует оси ординат ( y ), ось абсцис ( x ) строится автоматически от 0 до n, где n — это длинна массива ординат. Следующий код построит точно такой же график:

Такой способ может оказаться полезным, если диапазон чисел на оси абцис для вас не важен. Однако, если диапазон или шаг все-таки важны, то их все же необходимо указать:

Еще один интересный момент — числа в массиве абсцис не обязательно должны быть последовательными, т.е. могут быть абсолютно произвольными, а соединяться линией будут так же только последовательные точки. Например:

Такое поведение очень удобно, когда вам необходимо строить плоские, замкнутые кривые или геометрические фигуры:

Как вы заметили мы два раза использовали метод plt.plot() , передавая разные данные. С определенной натяжкой, можна сказать, что метод plt.plot() и занимается прорисовкой наших линий, а plt.show() отображением самого графика. Но мы оставим все подробности на потом и двинемся дальше.

2.2. График множества точек

Единственное отличие графика множества точек от графика линии — точки не соединяются линией. Вот и все.

Все как и прежде двум соответствующим значениям из массивов соответствуют координаты точки.

Если у вас несколько множеств, то все их так же можно построить на одном графике:

2.3. Гистограммы

Очень часто, данные удобно представлять в виде гистограмм. В самом простом случае, гистограмма — это множество прямоугольников, площадь которых (или высота) пропорциональна какой-нибудь величине. Например, осадки за 3 месяца: в июне выпало 10 мм, в июле — 15мм, в августе — 21 мм.

Первый массив содержит номера месяцев, а второй массив — значения показателей. Эти прямоугольники построены вертикально, но их можно отображать и в горизонтальном виде:

Гистограммы могут отображать несколько наборов данных, что очень удобно для их сравнения:

Такой график мог бы отображать летние осадки за два года. Но вот в чем дело, прямоугольники строятся поверх друг друга и если они равны, как в случае наших осадков за август, то прямоугольники друг друга перекроют. Если указать небольшое смещение по оси x, то ситуация не улучшится:

График станет привлекательней, если сузить прямоугольники и расположить их без наложения друг на друга:

2.4. Круговые диаграммы

Если вам необходимо наглядно отобразить соотношение частей целого, то лучше воспользоваться круговой диаграммой. Например, в компании работают 50 человек из них 40 женщи и 10 мужчин:

Все предельно просто — количество элементов в массиве определяет количество клиньев, а величина значений определяет их площадь:

2.5. Ящик с усами

Данный тип графиков действительно похож на ящик с усами (если повернуть монитор на 90 o ):

Но на самом деле этот ящик с усами является диаграммой размаха, служит для отображения случайной величины и несет в себе достаточно много информации. Во первых, внутри ящика оранжевой линией отмечена медиана элементов массива — это такое значение которое меньше и больше ровно половины элементов массива. В нашем случае, это значение равно 5.5 и как нетрудно заметить половина элементов меньше его, а другая больше. Его границами служат 25-й и 75-й процентили (4.25 и 6.75 для нашего массива). Ну а усами, собственно (как правило) максимальное и минимальное значение в наборе данных. Вот такой непростой, но очень полезный ящик.

Иногда на графике, рядом с усами появляются одна или две точки. Такие точки обозначают выбросы — значения которые находятся очень далеко от статистически значимой части данных:

Как не трудно догадаться, в основе данного типа графиков находится статистическая подоплека и наиболее полезен он именно в этой области.

2.6. Что дальше?

Мы построили несколько очень простых графиков и если вам нужно просто взглянуть на данные, то этих методов уже достаточно. Так же мы построили «ящик с усами» — достаточно сложный график, но и он строится по недвусмысленным, четким правилам. Да, matplotlib умеет строить очень сложные графики, например, графики автокорреляции или спектрограмм.

Но, преимущество данной библиотеки даже не в том что она может строить кучу разных графиков, а в том что она предоставляет полный контроль (хотя, полный вовсе не означает, что он простой) над всем, что может отобразить (полный не означает простой).

Собственно, теперь можно сделать следующий шаг — разобраться с магическими командами IPython для matplotlib и с тем как устроена область отображения графиков.

Источник статьи: http://pyprog.pro/mpl/mpl_types_of_graphs.html

matplotlib.pyplot.boxplot¶

Make a box and whisker plot.

Make a box and whisker plot for each column of x or each vector in sequence x . The box extends from the lower to upper quartile values of the data, with a line at the median. The whiskers extend from the box to show the range of the data. Flier points are those past the end of the whiskers.

notch : bool, optional (False)

If True , will produce a notched box plot. Otherwise, a rectangular boxplot is produced. The notches represent the confidence interval (CI) around the median. See the entry for the bootstrap parameter for information regarding how the locations of the notches are computed.

In cases where the values of the CI are less than the lower quartile or greater than the upper quartile, the notches will extend beyond the box, giving it a distinctive «flipped» appearance. This is expected behavior and consistent with other statistical visualization packages.

The default symbol for flier points. Enter an empty string (») if you don’t want to show fliers. If None , then the fliers default to ‘b+’ If you want more control use the flierprops kwarg.

vert : bool, optional (True)

If True (default), makes the boxes vertical. If False , everything is drawn horizontally.

whis : float, sequence, or string (default = 1.5)

As a float, determines the reach of the whiskers to the beyond the first and third quartiles. In other words, where IQR is the interquartile range ( Q3-Q1 ), the upper whisker will extend to last datum less than Q3 + whis*IQR ). Similarly, the lower whisker will extend to the first datum greater than Q1 — whis*IQR . Beyond the whiskers, data are considered outliers and are plotted as individual points. Set this to an unreasonably high value to force the whiskers to show the min and max values. Alternatively, set this to an ascending sequence of percentile (e.g., [5, 95]) to set the whiskers at specific percentiles of the data. Finally, whis can be the string ‘range’ to force the whiskers to the min and max of the data.

bootstrap : int, optional

Specifies whether to bootstrap the confidence intervals around the median for notched boxplots. If bootstrap is None, no bootstrapping is performed, and notches are calculated using a Gaussian-based asymptotic approximation (see McGill, R., Tukey, J.W., and Larsen, W.A., 1978, and Kendall and Stuart, 1967). Otherwise, bootstrap specifies the number of times to bootstrap the median to determine its 95% confidence intervals. Values between 1000 and 10000 are recommended.

usermedians : array-like, optional

An array or sequence whose first dimension (or length) is compatible with x . This overrides the medians computed by matplotlib for each element of usermedians that is not None . When an element of usermedians is None, the median will be computed by matplotlib as normal.

conf_intervals : array-like, optional

Array or sequence whose first dimension (or length) is compatible with x and whose second dimension is 2. When the an element of conf_intervals is not None, the notch locations computed by matplotlib are overridden (provided notch is True ). When an element of conf_intervals is None , the notches are computed by the method specified by the other kwargs (e.g., bootstrap ).

positions : array-like, optional

Sets the positions of the boxes. The ticks and limits are automatically set to match the positions. Defaults to range(1, N+1) where N is the number of boxes to be drawn.

widths : scalar or array-like

Sets the width of each box either with a scalar or a sequence. The default is 0.5, or 0.15*(distance between extreme positions) , if that is smaller.

patch_artist : bool, optional (False)

If False produces boxes with the Line2D artist. Otherwise, boxes and drawn with Patch artists.

labels : sequence, optional

Labels for each dataset. Length must be compatible with dimensions of x .

manage_ticks : bool, optional (True)

If True, the tick locations and labels will be adjusted to match the boxplot positions.

autorange : bool, optional (False)

When True and the data are distributed such that the 25th and 75th percentiles are equal, whis is set to ‘range’ such that the whisker ends are at the minimum and maximum of the data.

meanline : bool, optional (False)

If True (and showmeans is True ), will try to render the mean as a line spanning the full width of the box according to meanprops (see below). Not recommended if shownotches is also True. Otherwise, means will be shown as points.

zorder : scalar, optional (None)

Sets the zorder of the boxplot.

Returns: result : dict

A dictionary mapping each component of the boxplot to a list of the matplotlib.lines.Line2D instances created. That dictionary has the following keys (assuming vertical boxplots):

• boxes : the main body of the boxplot showing the quartiles and the median’s confidence intervals if enabled.
• medians : horizontal lines at the median of each box.
• whiskers : the vertical lines extending to the most extreme, non-outlier data points.
• caps : the horizontal lines at the ends of the whiskers.
• fliers : points representing data that extend beyond the whiskers (fliers).
• means : points or lines representing the means.

Other Parameters: showcaps : bool, optional (True)

Show the caps on the ends of whiskers.

showbox : bool, optional (True)

Show the central box.

showfliers : bool, optional (True)

Show the outliers beyond the caps.

showmeans : bool, optional (False)

Show the arithmetic means.

capprops : dict, optional (None)

Specifies the style of the caps.

boxprops : dict, optional (None)

Specifies the style of the box.

whiskerprops : dict, optional (None)

Specifies the style of the whiskers.

flierprops : dict, optional (None)

Specifies the style of the fliers.

medianprops : dict, optional (None)

Specifies the style of the median.

meanprops : dict, optional (None)

Specifies the style of the mean.

In addition to the above described arguments, this function can take a data keyword argument. If such a data argument is given, the following arguments are replaced by data[]:

• All positional and all keyword arguments.

Objects passed as data must support item access ( data[] ) and membership test ( in data ).

Источник статьи: http://matplotlib.org/3.1.0/api/_as_gen/matplotlib.pyplot.boxplot.html

📊 Ваша повседневная шпаргалка по Matplotlib

Matplotlib – наиболее широко используемый инструмент на Python. Он имеет отличную поддержку множеством сред, таких, как веб-серверы приложений, графические библиотеки пользовательского интерфейса, Jupiter Notebook, iPython Notebook и оболочка iPython.

Архитектура Matplotlib

Matplotlib имеет три основных слоя: слой нижнего уровня (backend), слой рисунков и слой скриптов. Слой нижнего уровня содержит три интерфейсных класса: канва рисунка (figure canvas), определяющая область рисунка, прорисовщик (renderer), умеющий рисовать на этой канве, и событие (event), обрабатывающее ввод пользователя вроде щелчков мыши. Слой рисунков знает, как рисовать с помощью Renderer’а и рисовать на канве. Все, что находится на рисунке Matplotlib, является экземпляром слоя рисунка (artist). Засечки, заголовок, метки – все это индивидуальные объекты слоя рисунков. Слой скриптов – это облегченный интерфейс, который очень полезен для ежедневного применения. Все примеры, приведенные в этой статье, используют слой скриптов и среду Jupiter Notebook.

Если вы используете эту статью для обучения, я рекомендую вам запускать каждый пример кода.

Подготовка данных

Подготовка данных – часто выполняемая задача перед любым проектом по визуализации данных или анализа данных, поскольку данные никогда не приходят в том виде, в котором они нам нужны. Я использую набор данных об иммиграции в Канаду. Сначала импортируем необходимые пакеты и набор данных.

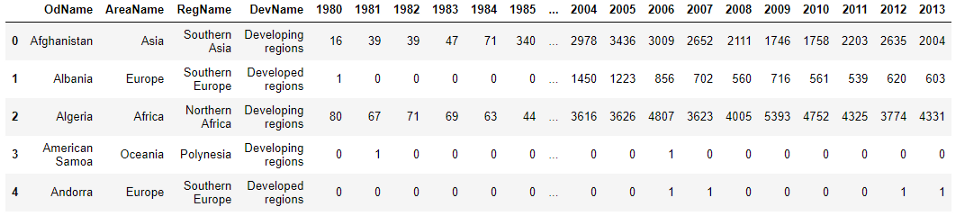
Я пропускаю первые 20 строк и последние две строки, потому что это текст, а не данные с табуляцией. Набор данных слишком велик, так что я не могу показать его целиком. Чтобы получить представление о наборе, давайте посмотрим на имена столбцов:

Мы не собираемся использовать все эти столбцы в нашей статье. Поэтому давайте избавимся от столбцов, которые мы не будем использовать, чтобы сделать набор данных меньшим и лучше управляемым.

Посмотрите на эти столбцы. Столбец ‘OdName’ – на самом деле название страны, ‘AreaName’ – континент, а ‘RegName’ – регион на этом континенте. Переименуем эти столбцы, чтобы их имена стали более понятными.

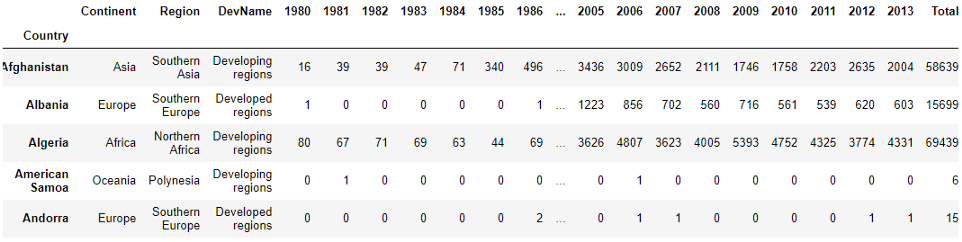
Теперь наш набор данных стал более простым для понимания. У нас есть Country, Continent, Region, а DevName указывает, является ли страна развитой или развивающейся. Все столбцы с годами содержат количество иммигрантов в Канаду из соответствующей страны за указанный год. Теперь добавим столбец ‘Total’ (‘Всего’), в котором будет содержаться общее количество иммигрантов из этой страны с 1980-го до 2013-го.

Посмотрите, в конце добавился новый столбец ‘Total’.

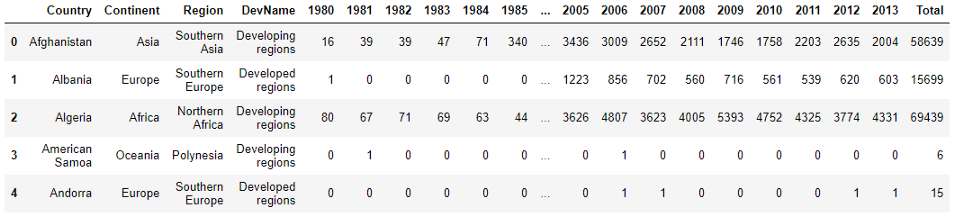
Проверим, есть ли в наборе какие-либо значения null.

Результат показывает 0 во всех столбцах, то есть в наборе нет пропусков. Я люблю задавать в качестве индекса значащий столбец, а не какие-то цифры, поэтому установим столбец ‘Country’ в качестве индекса.

Теперь набор данных достаточно чист и красив, чтобы начать работать с ним, поэтому больше чистить мы не станем. Если нам потребуется что-то еще, мы сделаем это по мере необходимости.

Упражнения по рисованию диаграмм

В этой статье мы попробуем несколько различных типов диаграмм – таких, как линейная диаграмма (line plot), диаграмма с областями (area plot), секторная диаграмма (pie plot), диаграмма рассеяния (scatter plot), гистограмма, столбчатая диаграмма (bar graph). Сначала импортируем необходимые пакеты.

Выберем стиль, чтобы нам не пришлось слишком утруждаться установкой стиля диаграммы. Вот список доступных стилей:

Я буду использовать стиль ‘ggplot’. Вы можете взять любой другой стиль по своему вкусу.

Линейная диаграмма

Будет полезным увидеть график изменений иммиграции в Канаду для одной страны. Создадим список лет с 1980-го до 2013-го:

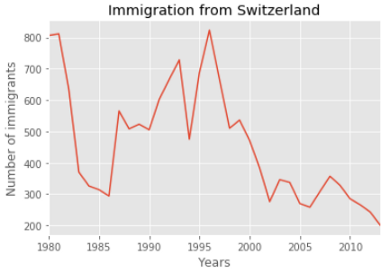
Я выбрала для этой демонстрации Швейцарию. Приготовим иммиграционные данные по нашим годам для этой страны.

Данные по иммиграции из Швейцарии (часть)

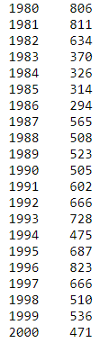
Настало время нарисовать диаграмму. Это очень просто: достаточно вызвать функцию plot для приготовленных нами данных. Затем добавим заголовок и метки для осей x и y.

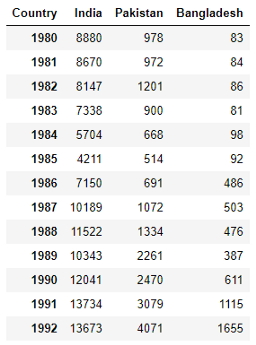
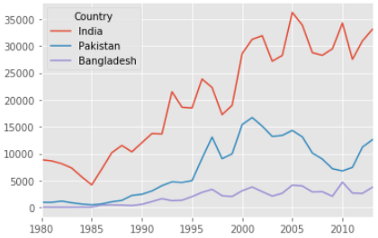
Что, если мы хотим вывести графики иммиграции для нескольких стран сразу, чтобы сравнить тенденции иммиграции из этих стран в Канаду? Это делается почти так же, как и в прошлом примере. Нарисуем диаграмму иммиграции из трех южно-азиатских стран: Индии, Пакистана и Бангладеш по годам.

Посмотрите на формат этих данных – он отличается от данных по Швейцарии, использованных прежде. Если мы вызовем функцию plot для этого DataFrame (ind_pak_ban), она выведет количество иммигрантов в каждой стране по оси x и годы по оси y. Нам нужно изменить формат данных:

Это не весь набор данных, а только его часть. Видите, теперь формат данных изменился. Теперь годы будут выводиться по оси x, а количество иммигрантов из каждой страны по оси y.

Нам не пришлось задавать тип диаграммы, потому что линейная диаграмма рисуется по умолчанию.

Секторная диаграмма

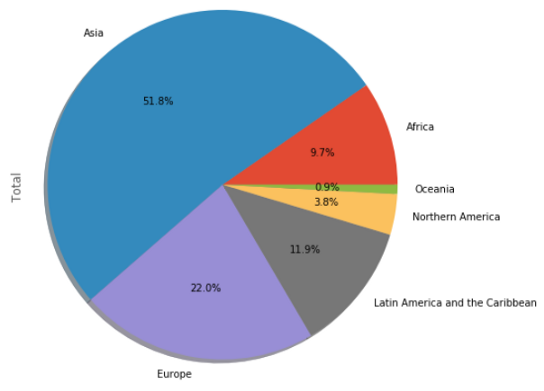
Чтобы продемонстрировать секторную диаграмму, построим диаграмму общего количества иммигрантов для каждого континента. У нас есть данные по каждой стране. Давайте сгруппируем данные по континентам, чтобы просуммировать количество иммигрантов для каждого континента.

Теперь у нас есть данные, показывающие общее количество иммигрантов для каждого континента. Если хотите, можете вывести этот DataFrame, чтобы увидеть результат. Я не привожу его потому, что он занимает слишком много места по горизонтали. Давайте нарисуем эту диаграмму.

Заметьте, что мне пришлось использовать параметр ‘kind’. Все виды диаграмм, кроме линейной, в функции plot нужно указывать явно. Я ввожу новый параметр ‘figsize’, определяющий размеры диаграммы.

Эта секторная диаграмма достаточно понятна, но мы можем сделать ее еще лучшей. На этот раз я установлю собственные цвета и начальный угол.

Разве эта диаграмма не лучше? Мне она нравится больше

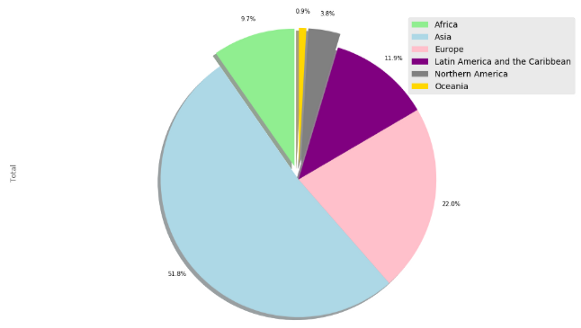
Ящик с усами (boxplot)

Сначала мы построим «ящик с усами» для количества иммигрантов из Китая.

Вот наши данные. А вот диаграмма, построенная по этим данным.

Если вам нужно освежить свои знания про «ящики с усами», пожалуйста, обратитесь к статье «Пример понимания данных с помощью гистограммы и ящика с усами».

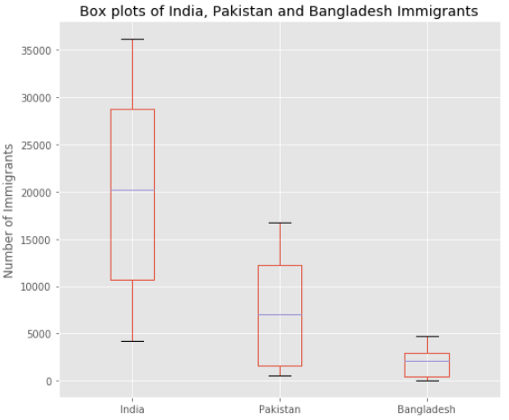
Мы можем нарисовать несколько ящиков с усами в одной диаграмме. Используем DataFrame ind_pak_ban и нарисуем ящики для количества иммигрантов из Индии, Пакистана и Бангладеш.

Диаграмма рассеяния

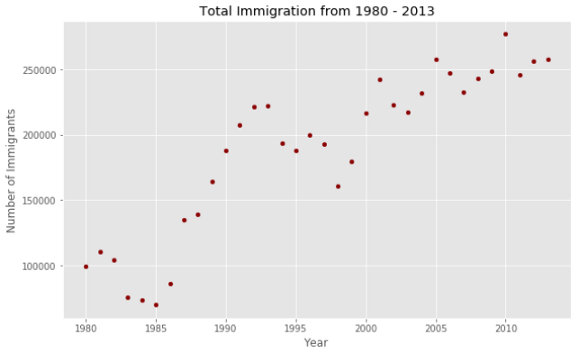
Диаграммы рассеяния лучше всего подходят для исследования зависимости между переменными. Построим диаграмму рассеяния, чтобы увидеть тренд количества иммигрантов в Канаду за годы.

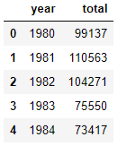
Для этого упражнения мы создадим новый DataFrame, содержащий годы в качестве индекса и общее количество иммигрантов за каждый год.

Нам нужно преобразовать годы в целые числа. Я также хочу немного причесать DataFrame, чтобы сделать его более презентабельным.

Осталось задать параметры осей x и y для диаграммы рассеяния.

Похоже, здесь есть линейная зависимость между годом и количеством иммигрантов. С течением лет количество иммигрантов показывает явно растущий тренд.

Диаграмма с областями

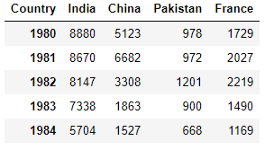
Диаграмма с областями показывает область под линейным графиком. Для этой диаграммы я хочу создать DataFrame, содержащий информацию по Индии, Китаю, Пакистану и Франции.

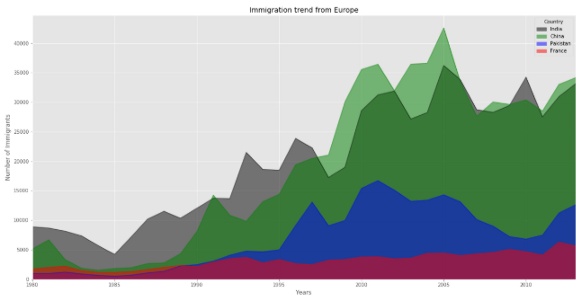
Набор данных готов. Пора сделать из него диаграмму.

Не забудьте использовать параметр ‘stacked’, если хотите увидеть области для каждой отдельной страны. Если не установить stacked = False, диаграмма будет выглядеть примерно так:

Если диаграмма stacked (по умолчанию), область, соответствующая каждой переменной, соответствует не расстоянию до оси x, а расстоянию до графика предыдущей переменной.

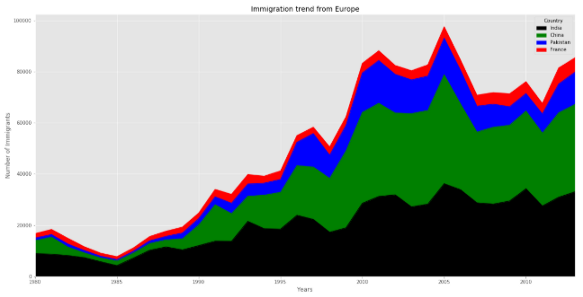
Гистограмма

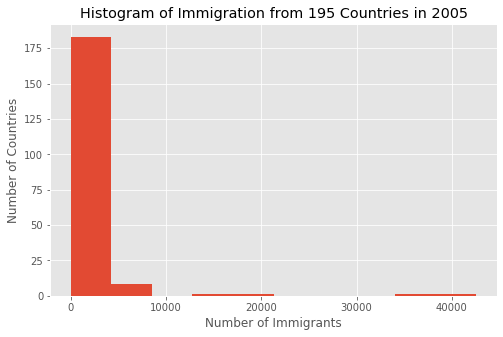
Гистограмма показывает распределение переменной. Вот ее пример:

Мы построили гистограмму, показывающую распределение иммиграции за 2005 год. Гистограмма показывает, что из большинства стран приехало от 0 до 5000 иммигрантов. Только несколько стран прислали 20 тысяч, и еще пара стран прислала по 40 тысяч иммигрантов.

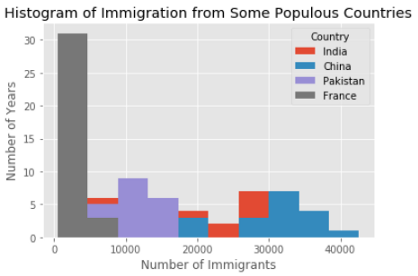
Давайте используем DataFrame top из предыдущего примера и нарисуем распределение количества иммигрантов из каждой страны в одной и той же гистограмме.

На предыдущей гистограмме мы видели, что из нескольких стран приехало 20 и 40 тысяч иммигрантов. Похоже, что Китай и Индия среди этих «нескольких». На этой гистограмме мы не можем четко увидеть границы между столбцами. Давайте улучшим ее.

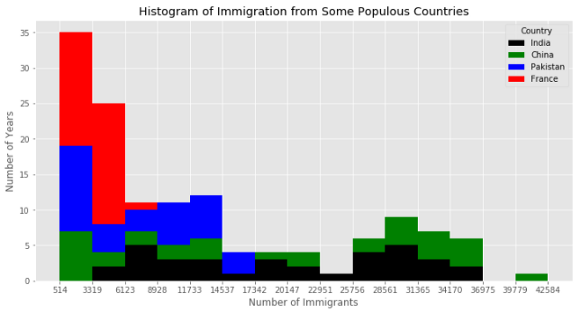
Задаем количество столбцов и показываем их границы.

Я использую 15 столбцов. Здесь я ввожу новый параметр под названием ‘alpha’ – он определяет прозрачность цветов. Для таких перекрывающихся диаграмм, как наша, прозрачность важна, чтобы увидеть картину каждого распределения.

Гистограмма с прозрачностью. Теперь мы можем увидеть каждое распределение.

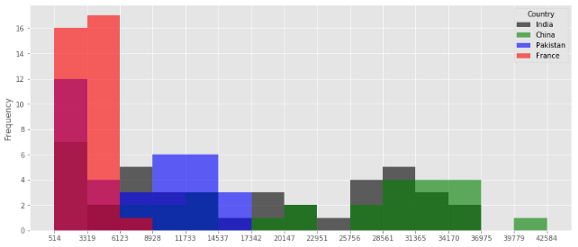
Как и для диаграммы с областями, мы можем использовать параметр ‘stacked’, но для гистограмм он по умолчанию выключен.

Столбчатая диаграмма

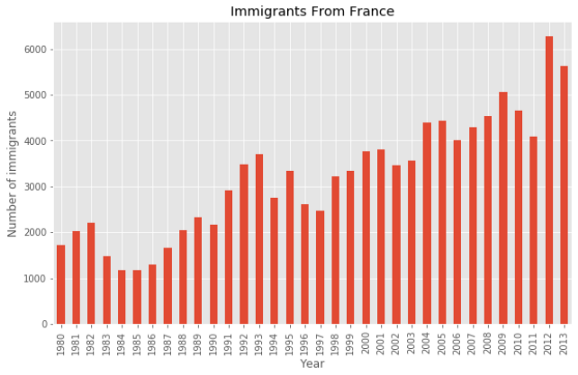
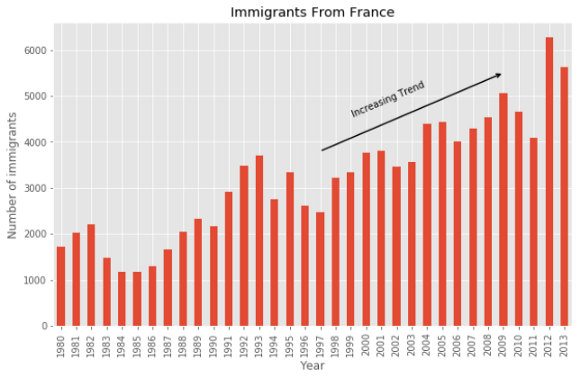
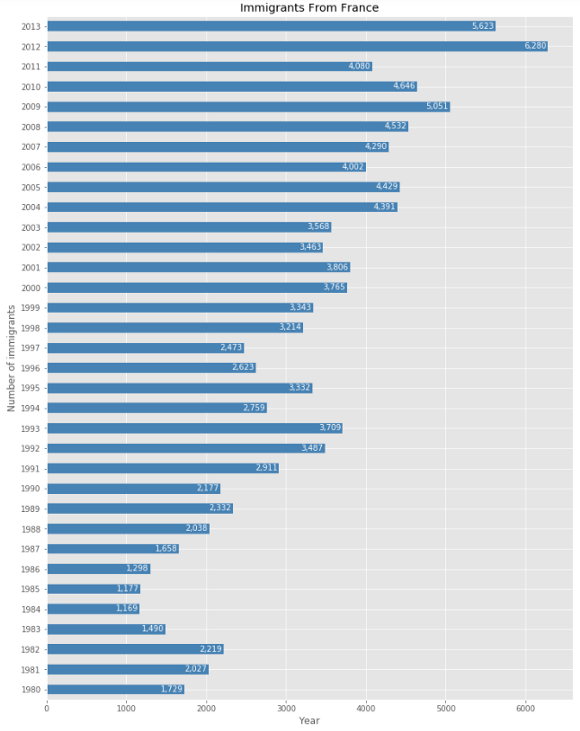
Для столбчатой диаграммы я использую количество иммигрантов из Франции за каждый год.

Вы можете добавить к столбчатой диаграмме дополнительную информацию. Эта диаграмма показывает растущий тренд с 1997 года примерно на декаду, который стоит отметить. Это можно сделать с помощью функции annotate.

Иногда горизонтальное расположение столбцов делает диаграмму более понятной. Еще лучше, если метки рисуются прямо на столбцах. Давайте сделаем это.

Разве эта диаграмма выглядит не лучше, чем предыдущая?

В этой статье мы изучили основы Matplotlib. Теперь у вас достаточно знаний, чтобы начать самостоятельное использование Matplotlib прямо сегодня.

Расширенные методы визуализации описаны в следующих статьях:

Источник статьи: http://proglib.io/p/vasha-povsednevnaya-shpargalka-po-matplotlib-2021-02-04