Ящики с усами spss

В SPSS – команда Boxplot (Ящичные диаграммы, «Ящики с усами»)

Это ящик с усами Пример выброса.

Для построения этой диаграммы используют так называемые 5 базовых показателей (медиану, квартили и наименьшее и наибольшее значения в выборке), несущих важную информацию как о диапазоне числовой оси, в котором оказались первичные данные, так и об их взаимном расположении внутри выборки. (см. вопрос 37) (источник сеть)

Проблема пропусков данных

Вопросы:

Допустимы ли пропуски?

Если допустимы, то:

n В какой доли случаев они допустимы?

В больших мультицентровых клинических исследованиях процент пропуска данных иногда достигает более 10% . На этапе планирования клинического испытания его возможная доля учитывается при расчете необходимого объема выборки и мощности статистических методов, применяемых для анализа данных. (Источник Тихова Г.П. Пропуск данных в выборке:как решать проблему и как ее избежать)

1.2. Что делать с пропусками?

Варианты решений:

l Исключить данные по переменной

l Исключить данные испытуемого

l Заполнить случайными значениями (не рекомендуется)

39. Анализ нормальности распределения переменных, основные способы.

Источник статьи: http://studopedia.ru/27_12227_v-SPSS—komanda-Boxplot-yashchichnie-diagrammi-yashchiki-s-usami.html

Диаграмма «ящик с усами» в статистике

Содержание:

Диаграмма «ящик с усами»

Построение диаграммы «Ящик с усами» рассмотрим на следующем примере

Задача пример №154

15 работников фирмы при сдаче экзамена по технике безопасности, получили следующие баллы:

13 9 18 15 14 21 7 10 11 20 5 18 37 16 17.

Представьте данную информацию в виде диаграммы «ящик с усами».

Решение:

1. Расположите данные в порядке возрастания, определите медиану и отметьте ее через .

2. Данные слева от медианы расположены в первой нижней половине, справа от медианы — в верхней половине. Т.е. медиана делит данные на две половинки.

3. Медианы половинок, называемые квартилями (здесь = 10, = 18), разбивают данные на 4 части.

4. Определяют изменение между квартилями — = 18 — 10 = 8

5. Отметим на числовой оси наименьшее и наибольшее значения, квартили и медиану — 5 важных точек. Нарисуем прямоугольник, длина которого равна разности изменению между квартилями. Этот прямоугольник делится медианой на две части. Теперь нарисуем «усы», соединив наибольшее и наименьшее значения с соответствующими квартилями.

Мы построили диаграмму «ящик с усами» в соответствии с представленными данными. Теперь, по диаграмме, представим данные. Из диаграммы видно, что приблизительно половина, 50 % , из 15 человек набрали от 10 до 18 баллов, 25% — меньше 10 баллов и 25% — больше 10 баллов.

Разница длин левого и правого «уса» зависит от разницы значений данных в соответствующих частях.

Для построении диаграммы «ящик с усами» из заданной совокупности выделяют 5 значений:

Медиану , квартиль , значение которого меньше медианы и является медианой нижней половины, квартиль , значение которого больше медианы и является медианой верхней половины множества данных, наибольшее и наименьшее значения.

Шаги построения диаграммы «ящик с усами»

1. Проводится горизонтальная прямая.

2. В зависимости от диапазона изменения данных проводится деление.

3. На прямой отмечают 5 значений — , , , наименьшее значение, наибольшее значение.

4. От до рисуется ящик.

5. Рисуем «усы» от : до минимального значения и от до максимального значения.

Задача пример №155

Ниже представлены данные возраста участниц женской паралимпийской команды по волейболу

24, 30, 30, 22, 25, 22, 18, 25, 28, 30, 25, 27. Представьте данные в виде диаграммы «ящик с усами».

Решение:

1. Расположим данные и найдем медиану и квартили.

2. Изобразим числовую ось и отметим эти следующие данные.

3. При помощи разности квартилей — = 29 -23 = 6 нарисуем ящик и разделим его на две части (при помощи медианы). Соединим ящик с наибольшим и наименьшим значением.

4. Представление диаграммы. Возраст 50% баскетболисток между 23-29 годами, 25% меньше 23 лет, 25% — больше 29 лет. Длинными или короткими являются «усы» ящика показывает, близко ли или далеко расположены друг от друга данные внутри 25% — го интервала. Например, левый «ус» длиннее, правый — короче. Так как в 25%-интервале значения изменяются между 18-23, а в левом «усе» мы встречаем только два значения 29-30.

Данные, которые сильно отличаются от основных данных совокупности, называются выбросами. Выбросы можно определить относительно верхнего и нижнего квартиля. В этом случае выбросом считается, значение в 1,5 раза больше или меньше разности — . Например, в рассмотренном нами примере нижний квартиль 23, верхний квартиль 29, разность квартилей 6. Тогда значения 23 — 1,5 • 6 = 14 и 29 + 1,5 • 6 = 38 считаются граничными значениями. Все значения, которые больше 38 и меньше 14, называются выбросами.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник статьи: http://natalibrilenova.ru/diagramma-yaschik-s-usami-v-statistike/

Как использовать SPSS для маркетингового статистического анализа: T-тестирование

Эти инструкции показывают, как использовать компьютерную программу «Статистический пакет для социальных наук» (SPSS), программную систему, используемую для анализа данных, для анализа статистики в маркетинге и других дисциплинах. В нем объясняется, как выполнить предварительный выборочный t-тест, когда предоставляется набор данных, и объясняется, как оценить значимость данных. Эти инструкции предназначены для лиц, имеющих базовые знания в области статистического анализа и методов исследования. Эти инструкции были созданы для использования с компьютером Windows и с использованием программы SPSS 24.

Шаг 1 Понимание Т-теста

Выполните образец T-теста на SPSS

» ‘Sample T-tes’ » t: Изучает доказательства того, что независимая переменная существенно влияет на зависимую переменную; если это так, то это статистически значимо.

» ‘Переменная’ »: элемент, функция или фактор, которые могут изменяться или изменяться.

» ‘Независимая переменная’ »: эта переменная отличается от каждого статистического теста и влияет на зависимую переменную.

» ‘Зависимая переменная’ »: переменная, которая будет измерена и затронута независимой переменной.

» ‘Когда его использовать’ »: t-критерий выборки используется для проверки того, поступает ли выборка из определенной совокупности, когда полная информация о совокупности недоступна.

» ‘Образец’ »: Часть населения, которая является разумным для анализа (т. Е. Группа из 1000 человек, получивших опрос из 200 000 человек).

» ‘Население’ »: общая группа, из которой берется выборка. Обычно он не может быть представлен напрямую, но вместо этого представлен косвенно через анализ образца.

Шаг 2 Открытие SPSS

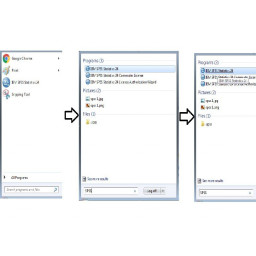
Нажмите на меню «Пуск» компьютера в нижнем левом углу вашего компьютера.

Перейдите к «Все программы».

Перейдите в раздел «Статистика IBM SPSS».

Дважды щелкните «IBM SPSS Statistics».

Представленная здесь версия IBM SPSS — IMB SPSS 24. На вашем компьютере может быть установлена ​​другая версия.

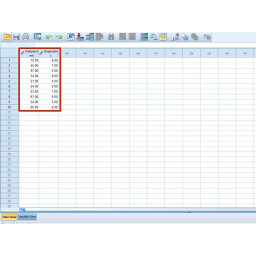
Шаг 3 Ввод данных

Выберите между использованием существующих данных или вводом данных вручную.

Существующие данные могут включать информацию, уже введенную в таблицу Excel. Данные, которые должны быть добавлены вручную, могут включать данные, еще не введенные в компьютерную программу.

Перейдите к шагу 4: «Использовать существующие данные», если у вас уже есть данные, необходимые для другой программы.

Переходите к шагу 5: «Ввод данных вручную», если ваши данные еще не были введены в программу.

Шаг 4 Использование существующих данных

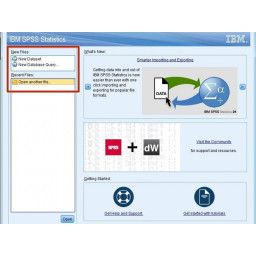
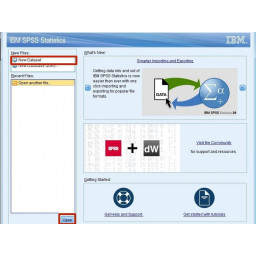
Нажмите «Открыть другой файл», как показано на рисунке 1.

Убедитесь, что для «Тип файлов» установлено значение «Все файлы».

Нажмите «Открыть» в нижней части окна.

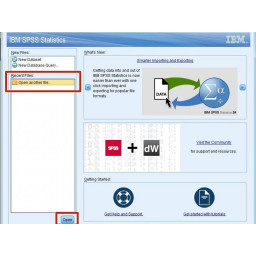
Нажмите на файл, который вы хотите загрузить.

Нажмите «Открыть», как показано на рисунке 2.

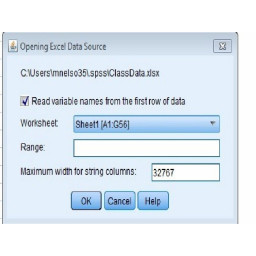
Нажмите «ОК», как показано на рисунке 3.

Если данные не представлены в числовой форме, их необходимо пометить. Перейдите к шагу 6, чтобы узнать, как это сделать.

Пропустите шаги 5 и 6. Перейдите к шагу 7.

Шаг 5 Ввод данных вручную

Нажмите на «Новый набор данных».

Данные, которые не представлены в числовой форме, должны быть помечены. Перейдите к шагу 6, чтобы узнать, как это сделать.

Шаг 6 Маркировка Номинальных Данных

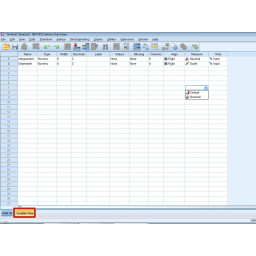
Переключитесь на «Variable View», как показано на рисунке 1.

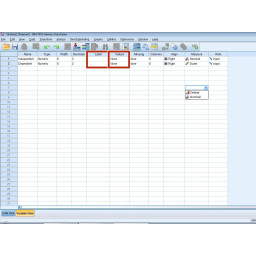
Введите метку вашей переменной в столбец «Метка», как показано на рисунке 2.

Нажмите на столбец «Значение», показанный на рисунке 2.

Следующие шаги показаны на рисунке 3.

Введите числовое значение, которое вы хотели бы использовать в поле «Значение».

Введите имя, которое представляет число в месте «Метка».

По завершении нажмите «ОК».

Шаг 7 Понимание представления данных

На этом экране отображаются все данные:

Верхняя строка содержит имена каждой из переменных.

Каждый столбец — это отдельная переменная.

Колонны — это вертикальные ящики.

Каждая строка — это данные, связанные с отдельным человеком.

Ряды — это горизонтальные ящики.

Нажмите на «Variable View» в левом нижнем углу страницы, показанной на рисунке 1.

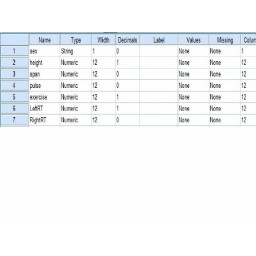
Шаг 8 Понимание Переменного Представления

В «Переменном виде»:

В первом столбце «Имя» указано имя переменной.

Второй столбец «Тип» указывает тип данных переменной.

Третий столбец, «Ширина», указывает количество символов, доступных для значений переменных.

Четвертый столбец «Десятичные знаки» определяет количество цифр после десятичного знака.

Пятый столбец, «Метка», используется для того, чтобы делать любые необходимые заметки.

Шестой столбец «Значения» предоставляет ключ для представления числовой переменной.

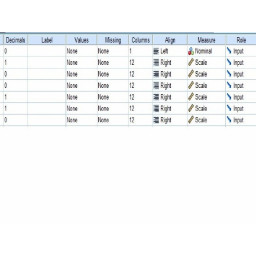
Шаг 9 Понимание представления переменных Продолжение

Седьмой столбец «Отсутствует» позволяет выбирать, включать или исключать значения из анализа.

Восьмой столбец, «Столбцы», указывает количество столбцов в переменной.

Девятый столбец «Выровнять» указывает выравнивание переменных.

В десятом столбце «Измерение» указывается уровень измерения переменной.

Последний столбец «Роль» определяет роль, которую переменная будет играть в анализе.

Шаг 10 Ввод данных и переменной

Если вы загрузили существующие данные, пропустите этот шаг и перейдите к шагу 11.

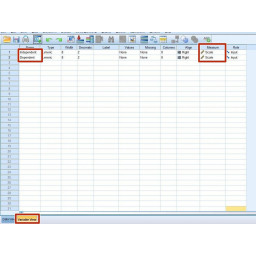
Убедитесь, что вы находитесь в «Variable View», проверив левый нижний угол экрана.

Поместите имя переменной в верхнюю левую ячейку (без пробелов) и убедитесь, что мера установлена ​​на «Масштаб», как показано на рисунке 1.

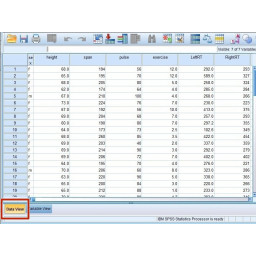
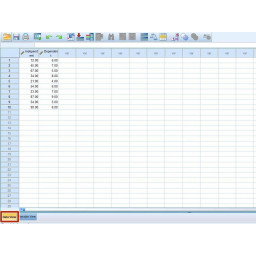
Переключитесь на «Просмотр данных», как показано на рисунке 2.

Находясь в «Представлении данных», подключите точки данных под столбцом, который вы только что отметили, как показано на рисунке 3.

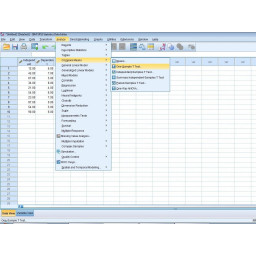
Шаг 11 Выполнение Т-теста

Нажмите вкладку «Анализ» в верхнем левом углу, как показано на рисунке 1.

Нажмите «Сравнить средства».

Нажмите «Один образец t-теста».

Переместите зависимую переменную, используя стрелку в середине экрана, как показано на рисунке 2.

Заполните тестовое значение пятно со средним населением.

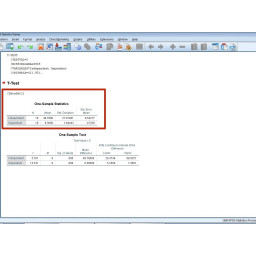
Шаг 12 Понимание результатов

Первый график — описательная статистика:

Первый столбец — количество участников.

Второй столбец — это среднее.

» ‘Среднее значение’ »: среднее значение из набора значений.

Третий столбец — стандартное отклонение.

«Стандартное отклонение»: мера ожидаемого отклонения результатов.

Четвертый столбец — стандартная ошибка среднего.

» ‘Стандартная ошибка’ »: распределение среднего значения выборки вокруг среднего значения популяции.

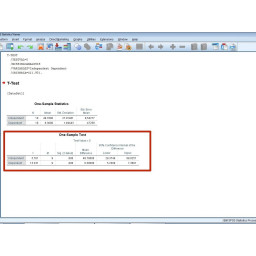
Шаг 13 Понимание результатов продолжение

Второй график — это t-тест:

Эта диаграмма поможет определить, являются ли результаты статистически значимыми.

Первый столбец — это оценка данных.

Второй столбец — это степени свободы.

Третий столбец — это значение sig данных.

» ‘P-value / sig’ » .: число, указывающее, где на стандартной кривой колокольчика должно быть значение, чтобы быть статистически значимым (если мы используем это, мы, вероятно, должны иметь изображение с ним)

Последние столбцы — это диапазоны внутри доверительных интервалов.

» ‘Диапазон доверительного интервала’ »: интервал, состоящий из диапазона значений, которые могут иметь неизвестный параметр.

Шаг 14 Анализ результатов

Определите, следует ли отклонить нулевую гипотезу, посмотрев на значение sig. Если значение sig меньше значения альфа, нулевая гипотеза отклоняется. Еще один способ определить, следует ли отвергнуть нулевую гипотезу, заключается в проверке доверительных интервалов. Если 0 не в этих интервалах, вы можете отклонить нулевую гипотезу.

» ‘Альфа-значение’ »: вероятность отклонения нулевой гипотезы, если она верна; часто равен р-значению

» ‘Нулевая гипотеза’ »: идея о том, что между указанными популяциями нет существенной разницы, любая наблюдаемая разница связана с выборкой или экспериментальной ошибкой

» ‘Альтернативная гипотеза’ »: идея о том, что существует существенная разница между указанными популяциями, причем любая наблюдаемая разница обусловлена ​​изменением переменной

Шаг 15 Интерпретация результатов

Чтобы интерпретировать результаты, посмотрите на значение p и значение альфа. Если p-значение меньше альфа-значения, нулевая гипотеза отклоняется. Если значение p больше, чем альфа, нулевая гипотеза принимается.

Запишите свои результаты в исследовательский документ, например: «Это не имеет значения. M = 48,70, SD = 27,01461, t (9) = 5,701, p Написать комментарий

Источник статьи: http://isfix.ru/manuals/84864-how-to-use-spss-for-marketing-statistical-analysis-t-testing.html